直线的倾斜角和斜率及直线方程练习
1、在下列四个命题中,正确的共有( )
(1)坐标平面内的任何一条直线均有倾斜角和斜率
(2)直线的倾斜角的取值范围是![]()
(3)若一条直线的斜率为![]() ,则此直线的倾斜角为
,则此直线的倾斜角为![]()
(4)若一条直线的倾斜角为![]() ,则此直线的斜率为
,则此直线的斜率为![]()
A.0个 B.1个 C.2个 D.3个
2、若两直线![]() 的倾斜角分别为
的倾斜角分别为![]() ,则下列四个命题中正确的是( )
,则下列四个命题中正确的是( )
A.
若![]() ,则两直线的斜率:
,则两直线的斜率:![]()
B.
若![]() ,则两直线的斜率:
,则两直线的斜率:![]()
C.
若两直线的斜率:![]() ,则
,则![]()
D.若两直线的斜率:![]() ,则
,则![]()
3、已知直线![]() 的倾斜角的正弦值是
的倾斜角的正弦值是![]() ,在
,在![]() 轴上的截距为
轴上的截距为![]() ,则
,则![]() 的方程是( )
的方程是( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
4、过两点![]() 和
和![]() 的直线在
的直线在![]() 轴上的截距为( )
轴上的截距为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
5、若直线![]() 在第一、二、三象限,则( )
在第一、二、三象限,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、已知![]() 直线
直线![]() 过点
过点![]() 且与线段MN相交,那么直线
且与线段MN相交,那么直线![]() 的斜率
的斜率![]() 的
的
取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、直线![]() 与两坐标轴所围成的三角形面积不大于1,那么( )
与两坐标轴所围成的三角形面积不大于1,那么( )
A.![]() B.
B.![]() C.
C.![]() 且
且![]() D.
D.![]() 或
或![]()
8、已知直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,且它的倾斜角是直线
,且它的倾斜角是直线
![]() 的倾斜角的2倍,则( )
的倾斜角的2倍,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9、若直线![]() 与两条直线
与两条直线![]() 分别交于P、Q两点,线段PQ的中点
分别交于P、Q两点,线段PQ的中点
坐标为![]() ,则
,则![]() 的方程是( )
的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10、若直线![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]() 的值( )
的值( )
A.2或3
B.2或![]() C.
C.![]() D.3
D.3
11、直线xtan![]() +y=0的倾斜角是( )
+y=0的倾斜角是( )
A.-![]() B.
B.![]() C.
C.![]() D.
D.![]()
12、直线![]() +
+![]() y+2=0的倾斜角范围是( )
y+2=0的倾斜角范围是( )
A.[![]() ,
,![]() )∪(
)∪(![]() ,
,![]() ] B.[0,
] B.[0,![]() ]∪[
]∪[![]() ,π)
,π)
C.[0,![]() ]
D.[
]
D.[![]() ,
,![]() ]
]
13、设直线ax+by+c=0的倾斜角为α,且sinα+cosα=0,则a、b满足( )
A.a+b=1 B.a-b=1 C.a+b=0 D.a-b=0
|
|
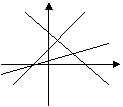 14、如图,直线
14、如图,直线
|
|
|
|
15、如图,直线![]() 的图象可能是( )
的图象可能是( )
![]()
![]()
|

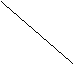
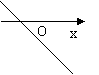 | |||||||||
A B C D
16、直线![]() 在两坐标轴上的截距之和为2,则实数
在两坐标轴上的截距之和为2,则实数![]() 的值为
的值为
17、点![]() 在直线
在直线![]() 上的射影为
上的射影为![]() ,则直线
,则直线![]() 的方程为
的方程为
18、求过点![]() ,且在两坐标轴上的截距互为相反数的直线
,且在两坐标轴上的截距互为相反数的直线![]() 的方程
的方程
19、直线![]() 经过点
经过点![]() 与
与![]() 轴、
轴、![]() 轴分别交于A、B两点,且AP:PB=3:5,
轴分别交于A、B两点,且AP:PB=3:5,
求直线![]() 的方程
的方程
20、已知直线l的斜率为6,且被两坐标轴所截得的线段长为![]() ,求直线l的方程.
,求直线l的方程.
21、已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P(2,3),求过两点Q1(a1,b1)、
Q2(a2,b2)(a1≠a2)的直线方程.
22、在直线方程y=kx+b中,当x∈[-3,4]时,y∈[-8,13],求此直线方程
直线的倾斜角和斜率及直线方程练习答案
1、A 2、D 3、C 4、A 5、D 6、C(提示:![]() 或
或![]() )7、C
)7、C
8、D 9、C 10、D
11、解析:k=-tan![]() =tan(π-
=tan(π-![]() )=tan
)=tan![]() 且
且![]() ∈[0,π)答案:D
∈[0,π)答案:D
12、解析:设直线的倾斜角为θ,则tanθ=-![]()
![]() .又-1≤cosα≤1,
.又-1≤cosα≤1,
∴-![]() ≤tanθ≤
≤tanθ≤![]() .∴θ∈[0,
.∴θ∈[0,![]() ]∪[
]∪[![]() ,π).答案:B
,π).答案:B
13、解析:0°≤α<180°,又sinα+cosα=0,α=135°,∴a-b=0.答案:D
14、D 15、A 16、![]() 17、
17、![]()
18、提示:分在两坐标轴上的截距为零和不为零两种情况进行讨论
19、解:由题意可知,直线![]() 的斜率存在,设为
的斜率存在,设为![]() ,点A、B的坐标分别为
,点A、B的坐标分别为![]() ,
,
故有(1)当![]() 时,点P在线段AB上,这时有
时,点P在线段AB上,这时有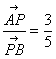 ,所以有
,所以有
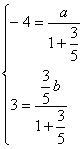 ,解得
,解得![]() ,这时直线
,这时直线![]() 的方程是:
的方程是:![]()
(2)当![]() 时,点P在线段BA的延长线上,这时有
时,点P在线段BA的延长线上,这时有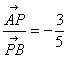 ,所以有
,所以有
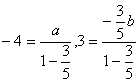 ,所以解得
,所以解得![]() ,这时直线
,这时直线![]() 的方程是:
的方程是:
![]() ,所以所求直线的方程是
,所以所求直线的方程是![]() 或
或![]()
20、解法一:设所求直线l的方程为y=kx+b.∵k=6,∴方程为y=6x+b.
令x=0,∴y=b,与y轴的交点为(0,b);令y=0,∴x=-![]() ,与x轴的交点为
,与x轴的交点为
(-![]() ,0).根据勾股定理得(-
,0).根据勾股定理得(-![]() )2+b2=37,∴b=±6.因此直线l的方程为y=6x±6.
)2+b2=37,∴b=±6.因此直线l的方程为y=6x±6.
21、剖析:利用点斜式或直线与方程的概念进行解答.
解:∵P(2,3)在已知直线上,
|
2a2+3b2+1=0.
∴2(a1-a2)+3(b1-b2)=0,即![]() =-
=-![]() .∴所求直线方程为y-b1=-
.∴所求直线方程为y-b1=-![]() (x-a1).
(x-a1).
∴2x+3y-(2a1+3b1)=0,即2x+3y+1=0.评述:此解法运用了整体代入的思想,方法巧妙.
思考讨论
依“两点确定一直线”,那么你又有新的解法吗?
提示: 由
![]() 2a1+3b1+1=0,
2a1+3b1+1=0,
2a2+3b2+1=0,
知Q1、Q2在直线2x+3y+1=0上.
![]() 22、解:当x的区间的左端点与y的区间的左端点对应,x的区间的右端点与y的区间的右端点对应时,得
22、解:当x的区间的左端点与y的区间的左端点对应,x的区间的右端点与y的区间的右端点对应时,得
![]()
|
4k+b=13 b=1 ∴直线方程为y=3x+1.
![]()
![]() 当x的区间的左端点与y的区间的右端点对应,x的区间右端点与y的区间的左端点对应时,得
当x的区间的左端点与y的区间的右端点对应,x的区间右端点与y的区间的左端点对应时,得
|
4k+b=-8, b=4.∴所求的直线方程为y=-3x+4.