高一下学期第一次月考数学试题
(2008-4-2)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列说法①终边相同的角必相等;②锐角必是第一象限角;③小于![]() 的角是锐角;④第二象限的角必大于第一象限的角;⑤若角
的角是锐角;④第二象限的角必大于第一象限的角;⑤若角![]() 的终边经过点M(0,-3),则角
的终边经过点M(0,-3),则角![]() 是第三或第四象限,其中错误的是( )
是第三或第四象限,其中错误的是( )
A.③④⑤ B. ①③④ C. ①③④⑤ D.②③④⑤
2.角α属于第二象限,且cos![]() =-cos
=-cos![]() ,则
,则![]() 角属于( )
角属于( )
A.第一象限的角 B.第二象限的角 C.第三象限的角 D.第四象限的角
3化简![]() 得到的结果是
( )
得到的结果是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4.已知集合A={![]() },B={
},B={![]() } ,则
} ,则![]() =( )
=( )
A、![]() B、{
B、{![]() } C、{
} C、{![]() } D、{
} D、{![]() }
}
5.设![]() ,其中
,其中![]() 都是非零实数,若
都是非零实数,若![]() 则f(2008)=( )
则f(2008)=( )
A、7 B、-7 C、1 D、-1
6.若![]() ,且
,且![]() ,则
,则![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7.
![]() ( )
( )
A.1 B.2 C.4
D.![]()
8. 已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9.在![]() 中,已知
中,已知![]() ,则该三角形是( )
,则该三角形是( )
A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰或直角三角形
10. ![]() ( )
( )
A、0
B、1 C、![]() D、
D、![]()
11.在![]() 中,如果
中,如果![]() 的大小为( )
的大小为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
12.已知![]() ,则
,则![]() 的范围是(
)
的范围是(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在题中横线上.
13. 已知![]() _________________
_________________
14.与![]() 终边相同且在
终边相同且在![]() 之间角是(用角度制表示)
之间角是(用角度制表示)
15.已知![]() ,则
,则![]() .
.
16. 若![]() ,则
,则![]() .
.
数学试题答题卷
 一、选择题(每小题5分,共60分)
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(每小题4分,共16分)
13 14
15 16
三、解答题:(本大题共6小题,共74分)
17. (本小题12分)
已知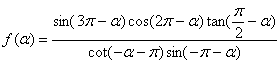
(1)化简![]() ;
;
(2)若![]() 是第四象限角,且
是第四象限角,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求
,求![]() 的值
的值
18.(本小题12分) 已知角θ的顶点与坐标原点O重合,其始边与χ轴正半轴重合,角θ的终边上有一点P(2t,-4t)(t≠0),求sinθ与cotθ的值.
19.(本小题12分)
已知![]() ,(1)求
,(1)求![]() 的值;
的值;
(2)求![]() 。
。
20. (本小题12分)已知![]() ,(1)求
,(1)求![]() 的值;
的值;
(2)求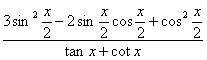 的值。
的值。
21.(本小题12分)
已知![]() 中,
中,![]() ,且
,且![]() ,
,
(1)求![]() 的大小;(2)求
的大小;(2)求![]() 的最小值,并求出此时
的最小值,并求出此时![]() 的大小。
的大小。
22.(14分)是否存在锐角α和β,使得①α+2β=![]() ; ②tanβ=(2-
; ②tanβ=(2-![]() )cot
)cot ![]()
同时成立?若存在,请求出α和β的值;若不存在,请说明理由.
数学试题参考答案
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | A | D | A | B | C | B | D | C | C | C |
二、填空题(每小题4分,共16分)
13 1 14
15 16
三。解答题
17.解(1)![]()
(2) ![]()
![]()
![]()
![]()
![]()
(3)![]()
18.解:![]()
(1)当t>0时,![]() ,
,![]() ,
, ![]()
(2) 当t<0时,![]() ,
,![]() ,
, ![]()
19.解:(1)![]()
![]()
![]() ,
,![]()
(2)![]()
![]()
![]()
![]()
![]()
20. 解:(1)![]()
![]()
![]()
![]()
![]()
(2)原式= 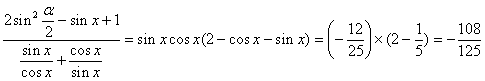
21.解:(1)由![]() 得,
得,![]()
![]()
![]()
![]()
(2)![]()
![]()
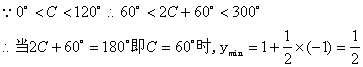
22 .由①得![]() 代入②得,
代入②得,![]()
即![]() ,整理得:
,整理得:![]()
![]()
![]() 时,
时,![]() .
.![]()
![]() 时,
时,![]()
![]() 存在
存在![]()