高一年级数学上册第一次月考试卷
一.选择题(每题4分,共40分)
1.如果集合![]() ,
,![]() ,那么┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
,那么┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A.![]() B.
B.![]()
![]()
![]() C.
C.![]() D.
D. ![]()
2.已知![]() ,则集合
,则集合![]() 中元素的个数是┄┄( )
中元素的个数是┄┄( )
A.![]() B.
B.![]() C.
C.![]() D.不确定
D.不确定
3.下列各组函数表示同一函数的是┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.函数![]() 的值域是┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
的值域是┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知函数![]() ,则
,则![]() 等于┄┄┄┄┄┄┄┄┄┄( )
等于┄┄┄┄┄┄┄┄┄┄( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数![]() 在区间
在区间![]() 上递减,则实数
上递减,则实数![]() 的取值范围是┄┄┄┄┄( )
的取值范围是┄┄┄┄┄( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知![]() ,且
,且![]() 则
则![]() 的值为┄┄┄┄┄┄┄┄( )
的值为┄┄┄┄┄┄┄┄( )
A.4
B.![]() C.
C.![]() D.
D.![]()
9.定义集合A、B的一种运算:![]() ,若
,若![]() ,
,![]() ,
,
则![]() 中的所有元素数字之和为┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
中的所有元素数字之和为┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄( )
A.9
B.![]() C.18
D.21
C.18
D.21
10.已知定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且在区间
,且在区间![]() 上是减函数,则( )
上是减函数,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二.填空题(每格4分,共16分)
11.函数![]() 的定义域为
.
的定义域为
.
12.已知函数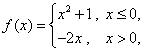 若
若![]() ,则
,则 ![]() .
.
13.已知函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域为
.
的定义域为
.
14.已知函数![]() 满足
满足![]() ,则
,则![]() .
.
三.解答题(本大题共6小题,满分64分)
15.(本题满分9分)
⑴ 用列举法表示集合![]() ;
;
⑵ 用描述法表示“比![]() 大,且比
大,且比![]() 小的所有实数”组成的集合
小的所有实数”组成的集合![]() ;
;
⑶ 用另一种方法表示集合![]() .
.
16.(本题满分11分)
⑴ 已知全集![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,![]() ,求集合
,求集合![]()
![]() ;
;
⑵ 已知集合![]() ,
,![]() ,若
,若![]() ,求实数
,求实数![]() 的值.
的值.
 17.(本题满分12分)
17.(本题满分12分)
已知函数![]()
⑴ 证明:函数![]() 是偶函数;
是偶函数;
⑵ 利用绝对值及分段函数知识,将函数解析式
写成分段函数,然后画出函数图像;
⑶ 写出函数的值域.
18.(本题满分12分)
已知函数![]()
⑴ 判断函数![]() 的单调性,并证明;
的单调性,并证明;
⑵ 求函数![]() 的最大值和最小值.
的最大值和最小值.
19.(本题满分10分)
已知函数![]() 是定义域在
是定义域在![]() 上的偶函数,且在区间
上的偶函数,且在区间![]() 上单调递减,
上单调递减,
求满足![]() 的
的![]() 的集合.
的集合.
20.(本题满分10分)
设![]() 是定义在
是定义在![]() 上的函数,对任意
上的函数,对任意![]() ,恒有
,恒有![]() ,
,
当![]() 时,有
时,有![]() .
.
⑴ 求证:![]() ,且当
,且当![]() 时,
时,![]() ;
;
⑵ 证明:![]() 在
在![]() 上单调递减.
上单调递减.

 高一年级数学上册第一次月考试卷答卷
高一年级数学上册第一次月考试卷答卷
一.选择题(每题4分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二.填空题(每格4分,共16分)
11. 12.
13. 14.
三.解答题(本大题共6小题,满分64分)
15.(本题满分9分)
16.(本题满分11分)
 17.(本题满分12分)
17.(本题满分12分)
18.(本题满分12分)
19.(本题满分10分)
 20.(本题满分10分)
20.(本题满分10分)
 高一年级数学上册第一次月考试卷参考答案
高一年级数学上册第一次月考试卷参考答案
一.选择题(每题4分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | A | C | C | D | B | B | A | B | B |
二.填空题(每格4分,共16分)
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]()
三.解答题(本大题共6小题,满分64分)
15.(本题满分9分)
解: ⑴ ![]() 3分
3分
⑵ ![]() 6分
6分
⑶ ![]() 9分
9分
16.(本题满分11分)
解: ⑴由![]() 图知:
图知:
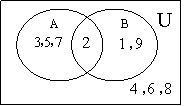
![]()
![]()
5分
⑵ 由于![]() 6分
6分
当![]() 时,有
时,有![]() 8分
8分
当![]() 时,有
时,有![]() ,又
,又![]()
![]()
![]() 10分
10分
![]() 11分
11分
17.(本题满分12分)
解: ⑴ 由于![]()
![]()
![]() 是偶函数 4分
是偶函数 4分
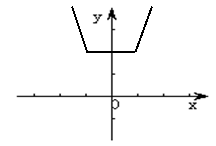 ⑵
⑵ 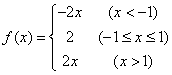 7分
9分
7分
9分
⑶ 由函数图象知,函数的值域为![]()
12分
18.(本题满分12分)
解:⑴ 设任取![]() 且
且![]()
![]() 5分
5分
![]()
![]()
![]() 即
即![]()
![]() 在
在![]() 上为增函数.
8分
上为增函数.
8分
⑵ 由⑴知,![]() 在
在![]() 上为增函数,则
上为增函数,则
![]()
![]() 12分
12分
19.(本题满分10分)
解: ![]() 在
在![]() 上为偶函数,在
上为偶函数,在![]() 上单调递减
上单调递减
![]() 在
在![]() 上为增函数 2分
上为增函数 2分
又![]() 4分
4分
![]()
![]() ,
,![]() 6分
6分
由![]() 得
得
![]()
![]() 9分
9分
![]() 解集为
解集为![]() .
10分
.
10分
20.(本题满分10分)
解: ⑴ 令![]() 得
得![]()
当![]() 时,有
时,有![]() ,
,![]()
![]() 2分
2分
当![]() 时,有
时,有![]() ,
,![]() ,又
,又![]()
![]() 5分
5分
⑵ 设![]() 且
且![]()
![]() 7分
7分
又![]() 9分
9分
![]()
![]()
![]() 在
在![]() 上单调递减.
10分
上单调递减.
10分