§4.10正切函数的图象与性质（二）
班级 学号 姓名
一、课堂目标：正切函数的图象及性质应用。
二、要点回顾：
1、正切函数的图象：
2、正切函数的性质：
| 正切函数 | |
| 定义域 | |
| 值域 | |
| 周期 | |
| 奇偶性 | |
| 单调性 |
2、不求值比较大小：
3、函数
的递增区间是
。
三、目标训练：
1、 函数
是
（ ）
（A）周期为
的奇函数 （B）周期为的偶函数 （C）周期为
的奇函数（D）周期为的偶函数
2、已知
，则
的大小关系是
（ ）
（A）
（B）
（C）
（D）
3、若
，则下列关系中成立的是
（ ）
（A）
（B）
（C）
（D）
4、函数
的图象与
的图象的交点个数是
（ ）
（A）2 （B）3 （C）4 （D）5
5、设直线
（a是常数）与函数
的图象相交，则相邻两个交点间的距离是（ ）
（A） （B）
（C）
（D）不能确定
6、若
，则必有
（ ）
（A）
（B）
（C）
（D）
7、已知
，且
则
。
8、函数
的周期是
，在区间
上是 函数。
9、求函数
的定义域、值域、并指出其周期、奇偶性和单调性。
10、求函数
的单调递减区间。
11、如果对于任意一个整数n，在区间
内至少有4个使函数
的值不存在的点，试求
的最小整数值。
12、已知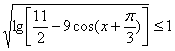
，求函数
的值域。