正弦

§5.10解斜三角形应用举例

班级　　　　 学号　　　　　  姓名　　　　　  

一、课堂目标：

掌握利用正弦定理及余弦定理解任意三角形的方法，懂得解任意三角形的知识在实际中有着广泛的应用，从而培养分析问题、解决问题的能力

二、要点回顾：

首先仔细分析题意，分清已知与所求，根据题意画出示意图．然后正确选择、运用正弦定理和余弦定理，在演算过程中，要算法简练，算式工整，计算正确，书写示范，严格要求自己．

三、目标训练：

1、在某次测量中，在A处测得同一方向的B点的仰角为60^O，点的俯角为70^O，则BAC等于（　　）

A.10^O　　　　　　　　　　　　　 B.50^OC.120^OD.130^O

2、有一长为1 km的斜坡，它的倾斜角为20^o，现要将倾斜角改成10^o，则斜坡长为（　　）

A.1　　　　　　　　　　　　　　　B.2sin 10^o　　　　　　　　　　 C.2cos 10^o　　　　　　　　　 D.cos 20^o

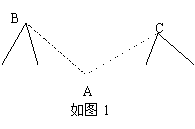3、如图1在山下A处用激光测距仪测出到两座山峰B、C的距离分别是2500m和2300m，从A处观察这两目标的视角是125^o，B、C两山峰相距多远？

4、 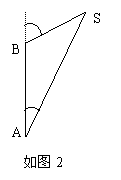 如图2，一艘船以32.2 n mile/h的速度向正北航行，在A处看灯塔S在船的北偏东20^o，30 min后航行到B处，在B处看灯塔S在船的北偏东65^o方向上，求灯塔S和B处的距离（精确到0.1 n mile）

5、 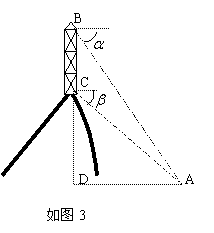 如图3，在山顶铁塔上B处测得地面上一点A的俯角=60^o，在塔底C处测得点A的俯角=45^o，已知铁塔BC部分高30m，求山高CD (精确到1m)

6、  如图4，飞机的航线和山顶在同一个铅直平面内，已知飞机的高度为海拔20000 m，速度为200 km/h，飞行员先看到山顶的俯角为20^o，经过1000 s后又看到山顶的俯角为81^o，求山顶的海拔高度（精确到1 m）