§5.10解斜三角形应用举例 (2)
班级 学号 姓名
1、在某海滨城市附近海面有一台风，经检测，当前台风中心位于城市O的东偏南
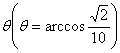方向300 km的海面P处，并以20 km/h的速度向西偏北45o方向移动，台风侵袭的范围为圆形区域，当前半径为60 km，并以10 km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？
2、在一个很大的湖岸边（可认为湖岸为直线）停放着一只小船，由于缆绳突然断开，小船被风刮跑，其方向与河岸成15o，速度为2.5 km/h，同时岸上有一人，从同一地点开始追赶小船，已知他在岸上跑的速度为4 km/h，在水中游的速度为2 km/h，问此人能否追上小船？若小船速度改变，则小船能被人追上的最大速度是多少？
3、A、B、C是一条直路上的三点，AB=BC=1 km,从这三点分别遥望一座电视发射塔P，A见塔在东北方向，B见塔在正东方向，C见塔在南偏东60O方向，求塔到直路的距离。
4、在海岸A处，发现北偏东45O方向，距A为
km的B处有一艘走私船，在A处北偏西75O方向，距A为2 km的C处的缉私船奉命以10
km/h的速度追截自私船，此时自私船正以10 km/h的速度从B处向北偏东30O方向逃窜，问缉私船沿什么方向能最快追上自私船，并求出所需要的时间。
5、有一块扇形铁板，半径为R，圆心角为60O，工人师傅需从扇形中切割下一个内接矩形，求内接矩形的最大面积.
6、某登山队在山脚测得山顶的仰角是30o，沿斜角为20o的斜坡前进1千米后，又测得山顶的仰角是60o，求山高
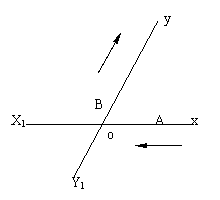7、如图，有两条相交成60角的直线xx1、yy1，交点是O，甲、乙分别在Ox、Oy上，起初甲位于离O点3 km的A处，乙位于离O点1mk的B处，后来两人同时用每小时4km的速度，甲沿xx1的方向，乙沿y1y的方向步行
（1） 起初，两人的距离是多少？
（2） 用包含t的式子表示t小时后两人的距离
（3） 什么时候两人的距离最短?