正弦3

§5.10解斜三角形应用举例 (3)

班级　　　　 学号　　　　　  姓名　　

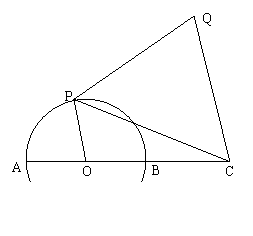1、已知C为半圆O的直径AB延长线上一点，且AO=OB=BC=2，P为半圆周上的一动点，以PC为边向外作等边三角形PCQ，如图1，问：何时四边形OCQP的面积最大？最大面积是多少？

2、P、Q是海上的两个灯塔，从海图上可测知，以PQ为弦，含圆周角为45^O的弓形狐内是危险区，内有许多暗礁，一海轮开始是，见到两个灯塔都在它的北偏东60^O，海轮向东行使一段距离后，见灯塔P恰在它的正北方向，灯塔Q在它的北偏东m^O(sin m⁰=)，问海轮继续向东航行是否有触礁的危险

3、若ABC的三边为a、b、c满足，则f (x)的图象　　　　　　（　　）

A.与x轴相切　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.在x轴上方

C.在x轴下方　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.与x轴交于两点

4、O为ABC的中心，AB=a, 过O的直线交AB于M，交AC于N，求的最大值和最小值.

5、设2a+1,a,2a-1为钝角三角形的三边，那么a的取值范围是多少？

6、ABC中,a+b=10,且cosC是方程2x²-3x-2=0的一个根，求ABC周长的最小值。

7、如图2，为了测量隧道道口AB的长度，给定下列四组数据，测量是应当用数据 　　　　　　　　　 （　　）

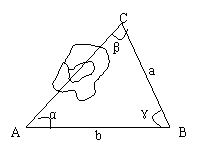A.　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　　　　　　　　　　　　　　　　　　　　　　　　　D.

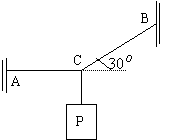8、如图，在一细绳C点系一重物P，细绳两端A、B分别固定在墙面上，使得AC保持水平，BC与水平方向成30角，已知细绳最大只能承受200牛顿的拉力，那么C点悬挂物的重量最多为多重？这时细绳的哪一端将断裂？

	A

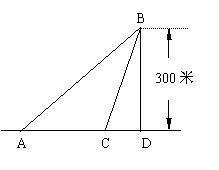9、如图，某海滨浴场的岸边可近似地看成直线，位于岸边A处的救生员发现海中B处有人求救，救生员没有直接从A处游向B处，而是沿岸边自A跑到距离B最近的D处，然后游向处B，若救生员在岸边的行进速度为6米/秒，在海中的行进速度为2米/秒，

（1）分析救生员的选择是否可行？

（2）在AD上找一处，使救生员从A到B的时间为最短，并求出最短时间