正弦、余弦函数的奇偶性

　§4.8正弦、余弦函数的奇偶性

班级　　　　 学号　　　　　  姓名　　　　　  

一、　　　　　　 课堂目标：

掌握函数奇偶性的定义，会判断正弦、余弦函数及其它简单函数的奇偶性

二、　　　　　　 要点回顾：

奇函数定义：一般地，如果对于函数f(x)的定义域内的________________ ,都有____________ 成立，

则称f(x)为这一定义域内的奇函数，奇函数的图象关于______________对称

偶函数定义：一般地，如果对于函数f(x)的定义域内的________________ ,都有____________ 成立，

则称f(x)为这一定义域内的偶函数，偶函数的图象关于______________对称

正弦函数是______________，余弦函数是______________

若某个函数是奇函数（或偶函数），则其定义域必须是________________

三、　　　　　　 目标训练：

1、  判断下列函数的奇偶性：

（1）y=_______________　 (2) y=______________  (3) y=3cosx+1_______________

　　　　 (4)　y=sinx - 1 ________________　

(5) y=xsin(n+x)　(nZ)　　　　　　　　　　　　　　　　　(6)y=

(7)y=　　　　　　　　　　　　　　　　　　　　　　　　　　(8)y=

　　　 （9）y=　　　　　　　　　　　　　　　　　　　 (10)y=sin(cosx)

　　　 2、下列命题中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

　　　 A.y= - sinx为偶函数　　　　　　　　　　　　　　　　　　　　　　　B.y=是非奇非偶

　　　 C.y=3cosx+1为偶函数　　　　　　　　　　　　　　　　　　　　　 D.y=sinx为奇函数

　　　 3、下列既是（0，）上的增函数，又是以为周期的偶函数是　　　　　　　　　　　　　　　　　　　　 (　　)

　　　 A.y=x²B.y=　　　　　　　　　 C.y=cos2x　　　　　　　　　　 D.y=e ^sin2x

　　　 4、函数f(x)是以4为周期的奇函数，且f(-1)=1，则sin的值为　　　　　　　　　　　(　　)

　　　 A.-1　　　　　　　　　　　　　　　　 B.0　　　　　　　　　　　　　　 C.1/2　　　　　　　　　　　　　 D.1

5、指出下列函数的奇偶性

（1）f(x)=3x　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2)f(x)=

(3)　f(x)=　　　　　　　　　　　　　　　　　　　　　　　　　　 (4) f(x)=2x²+3　

(5)　f(x)=　　　　　　　　　　　　　　　　　　 (6) f(x)=

6、设函数y=f(x)的定义域是R，且y=f(x)既是奇函数又是偶函数，求f(x)的解析式

7^#、判断下列函数的奇偶性

（1）f(x)=　　　　　　　　　　　　　　　　　　(2)　f(x)=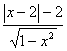

(3) f(x)=