高中代数“数列、极限、数学归纳法”检查题
（答题时间100分，满分100分）
一、（每小题4分，共40分）选择题
（1）数列1，3，…，82，…是（ ）
（A）等差数列，而不是等比数列 （B）等比数列，而不是等差数列
（C）等差数列，又是等比数列 （D）即非等差数列，也非等比数列
（2）已知
为等比数列，当
时，则
（ ）
（A）6 （B）7 （C）8 （D）9
（3）设数列
的前
项的和为
则
（ ）
（A）
（B）
（C）
（D）
（4）在等差数列
中，已知
设
则
（ ）
（A）8 （B）9 （C）10 （D）11
（5）已知首项为1的无穷等比数列的所有项之和为3，
为其公比，则=（ ）
（A）
（B）
（C）
（D）
（6）设无穷等比数列所有奇数项之和为15，所有偶数项之和为
为其首项，则
（ ）
（A）
（B）
（C）
（D）
（7）设数列的前项和
如果
则
（ ）
（A）
（B）
（C）
（D）
（8）已知
成等比数列，如果
和
都成等差数列，则
（ ）
（A）1 （B）2 （C）3 （D）4
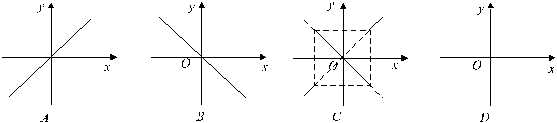
（9）函数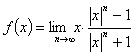
的图象是（ ）
|
|
（10）设
为方程
的两个有理根。则
（ ），
（ ）。
（A）
（B）
（C）
（D）
二、（每小题5分，共20分）填空题
（1）
填上第四项与第项
（A）
（B）
（C）
（2）
设数列：
的前项和为
（3）
设
成等差数列，且
则
（4）
已知数列：
的前项和为
三、（10分）设是200与300之间7的倍数的个数，试求：
（1）是什么数？
（2）这个7的倍数之和是多少？
四、（10分）某正数乘以
，误认为乘以
产生误差
，求此正数。
五、（10分）求数列
的前项的和。
六、（10分）设
用数学归纳法证明：
