§5.6平面向量的数量积及运律（二）
班级 学号 姓名
一、课堂目标：⑴利用向量的数量积求向量的长度，夹角问题；
⑵利用向量的数量积性质解决综合问题。
二、要点回顾：
1．由
可知，若
，
10，则
，
。
2．由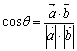
可知，若，10，则
与
的夹角为
=
。
3．由
可知，若，
，
。
三、目标训练
1．如果
，那么与的夹角为………………………………（ ）
A.
B.
C.
D.或
2.若
,则与的夹角的范围是…………………………………………………（ ）
A.
B. 
C.
D.
3.已知
且与的夹角,则
等于……………………………………（ ）
A.
B.
C.
D. 
4.已知,和实数
,下列等式中错误的是…………………………………………………（ ）
A.
B.
C.
D.
5.已知△ABC中,
则与的夹角为( )
A.
B.
C.
D.或
6.若
，
，求：
⑴. 
⑵. 
⑶. 
的最小值
7．已知
，与的夹角，求下列向量的夹角：
⑴.
与
⑵.
与
⑶．若
与
的夹角是锐角，则求的取值范围 。
8．已知与都是非零向量，求满足下列条件的与的夹角：
⑴
⑵