 期末复习----三角函数(一)
期末复习----三角函数(一)
班级 学号 姓名
一、复习目标:⑴熟练掌握诱导公式及和、差、倍、半公式;
⑵会利用公式进行化简、求值、证明。
二、目标训练:
1.已知![]() ,则
,则![]() 的值是……………………………………………( )
的值是……………………………………………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设![]() ,则
,则![]() 的取值范围是……………………………………( )
的取值范围是……………………………………( )
A.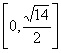 B.
B.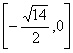 C.
C.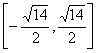 D.
D.![]()
3.已知![]() 那么
那么![]() 的值是……( )
的值是……( )
A.1
B.![]() C
C![]() D. 0
D. 0
4.已知![]() 满足①
满足①![]() ,②
,②![]() 则
则![]() 的值为…………………………………………………………………………………( )
的值为…………………………………………………………………………………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.一个直角三角形内角的正弦值成等比数列,其最小内角为…………………………………( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6.已知![]() ,则
,则![]() .
.
7.已知![]() ,则
,则![]() ,
,![]() .
.
8已知![]() ,则
,则![]() .
.
9.已知锐角![]() 满足
满足![]() 是方程
是方程![]() 的两根,则
的两根,则![]() 。
。
10.化简:![]() ,其中
,其中![]()
11.已知![]() ,求:(1)
,求:(1)![]() 的值;(2)
的值;(2)![]() 的值。
的值。
12.已知![]() 为锐角,且
为锐角,且![]() ,求证:
,求证:![]() .
.
13.是否存在锐角![]() 使得下列两式:①
使得下列两式:①![]() ②
②![]() 同时成立?若存在,求出
同时成立?若存在,求出![]() 和
和![]() ;若不存在,说明理由.
;若不存在,说明理由.
14.已知![]() 且
且![]() ,
,
(1)求使![]() 的
的![]() 的集合;
的集合;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值。
的值。
 期末复习----三角函数(二)
期末复习----三角函数(二)
班级 学号 姓名
二、复习目标:熟练掌握三角函数的图象与性质;会利用图象与性质进行解题。
二、目标训练:
1.函数![]() 的图象中的一条对称轴方程为…………………………………( )
的图象中的一条对称轴方程为…………………………………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.函数![]() 的值域为………………………………………………………( )
的值域为………………………………………………………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3函数![]() 的最大值为M,最小值
的最大值为M,最小值![]() ,则………………( )
,则………………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.当![]() 时,函数
时,函数![]() 的…………………………………
( )
的…………………………………
( )
A.最大值是1,最小值是![]() B.最大值是1,最小值是
B.最大值是1,最小值是![]()
C.最大值是2,最小值是![]() D.最大值是2,最小值是
D.最大值是2,最小值是![]()
5.若函数![]() 对任意
对任意![]() 都有
都有![]() ,则
,则![]() 等于 ( )
等于 ( )
A.3或0 B.-3或0 C.0 D.3或-3
6.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再作关于
个单位后,再作关于![]() 轴的对称图象,得到函数
轴的对称图象,得到函数
![]() 的图象,则
的图象,则![]() 可以是……………………………………………………( )
可以是……………………………………………………( )
A.![]() B.
B.![]() C.
C. ![]() D
D![]()
7.关于![]() 的不等式
的不等式![]() 的解集是
.
的解集是
.
8.
函数![]() 的单调减区间为
.
的单调减区间为
.
9.函数![]() 满足
满足![]() ,则
,则![]() .
.
10.利用五点法作出函数![]() 的图象,并指出此函数的振幅,周期,初相,频率,单调
的图象,并指出此函数的振幅,周期,初相,频率,单调
递增区间.
11.已知函数![]() 在同一周期内,当
在同一周期内,当![]() 时取得最大值
时取得最大值![]() ,
,
当![]() 时取得最小值
时取得最小值![]() ,求该函数的解析式.
,求该函数的解析式.
12.已知函数![]() .
.
⑴求函数![]() 的最小正周期;
的最小正周期;
⑵求函数![]() 的最大值及相应
的最大值及相应![]() 的取值集合;
的取值集合;
⑶函数的图象是否存在对称中心?若存在写出其中的一个(不必证明),若不存在,说明理由.
13.已知![]() ,当方程
,当方程![]() 有两个不相等的实数根时,(1)求
有两个不相等的实数根时,(1)求![]() 的取值范围;(2)求方程的两实根之和。
的取值范围;(2)求方程的两实根之和。