《向量》复习(2)
基本知识:
1. 点P分有向线段![]() 所成的比的
所成的比的![]() :
: ![]() ,或
,或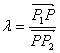
P内分线段![]() 时,
时, ![]() ; P外分线段
; P外分线段![]() 时,
时, ![]() .
.
2. 定比分点坐标公式:
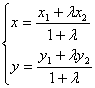
![]() ,中点坐标公式:
,中点坐标公式: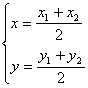
3. 三角形重心公式及推导(见课本例2):
三角形重心公式:![]()
4. 图形平移:设F是坐标平面内的一个图形,将F上所有的点按照同一方向移动同样长度(即按向量![]() 平移),得到图形F`,我们把这一过程叫做图形的平移。
平移),得到图形F`,我们把这一过程叫做图形的平移。
平移公式:![]() 或
或 ![]() 平移向量
平移向量![]() =
=![]() =(h,k)
=(h,k)
一.选择题(6分×10=60分):
1. 下列命题中不正确的是 ( )
A、若![]() =
=![]()
![]() ,则
,则![]() ∥
∥![]() B、若
B、若![]() ·
·![]() =0,则
=0,则![]() =0或
=0或![]() =0
=0
C、若![]() +
+![]() =0 ,则
=0 ,则 ![]() =
=![]() =0 D、若(
=0 D、若(![]() -
-![]() )2=0,则
)2=0,则
![]() =
=![]() 。
。
2. 三角形ABC中,设![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,若
,若![]() ·(
·(![]() +
+ ![]() )
)![]() ,则三角形
,则三角形
ABC是 ( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、无法确定其形状
3. 若![]() ·
·![]() =0,则
( )
=0,则
( )![]()
A.![]() =0或
=0或![]() =0 B.
=0 B.![]() 、
、![]() 的夹角是90
的夹角是90![]() C.A、B中至少有一种情况成立 D.
C.A、B中至少有一种情况成立 D.![]() =0且
=0且![]() =0
=0
4. 已知![]() =(1,2),
=(1,2),![]() =(x,1),且
=(x,1),且![]() +2
+2![]() 与2
与2![]() -
-![]() 平行,则x=
( )
平行,则x=
( )
A、2 B、1 C、![]() D、
D、 ![]()
5. 点A(m,n)关于点B(a,b)对称点的坐标是( )
A.(-m,-n) B.(a-m,b-n) C.(a-2m,b-2n) D.(2a-m,2b-n)
6. 已知![]() =(-4,3),
=(-4,3),![]() 是垂直
是垂直![]() 的单位向量,则
的单位向量,则![]() 等于
( )
等于
( )
A、(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
B、(
)
B、(![]() ,
,![]() )或(-
)或(-![]() , -
, -![]() )
)
C、(![]() ,-
,-![]() )或(-
)或(-![]() ,
,![]() ) D、(
) D、(![]() ,-
,-![]() )或(-
)或(-![]() ,
, ![]() )
)
7. 已知点A(1,2)、B(4,5),点C分线段AB成两部分,其中![]() =
=![]()
![]() ,则
,则
![]() 的值是
( )
的值是
( )
A、![]() B、-
B、-![]() C、
C、![]() D、-
D、-![]()
8. 线段AB的端点为A(x,5)、B(-2,y),直线AB上的点C(1,1),使![]() =2
=2![]() 则x,y的值是
( )
则x,y的值是
( )
A、7,-1 B、-5,3 C、7,3或-1,-5 D、7,-1或-5,3
9. 三角形ABC的两个顶点A(3,7)、B(-2,5),若AC的中点在x轴上,BC的中点在y轴上,则顶点C的坐标是 ( )
A、(2,-7) B、(-7,2) C、(-3,-5) D、 (-5,-3)
10. 已知O为坐标原点,点A、B的坐标分别是(a,0)、(0,a),其中常数a![]() 0,点P在线段AB上,且
0,点P在线段AB上,且![]() =t
=t![]() (0
(0![]() t
t![]() 1),则
1),则![]() ·
·![]() 的最大值是
( )
的最大值是
( )
A、a2 B、a C、 2a D、3a
二. 填空题(6分×10=60分):
11. 已知![]() =4,
=4,![]() 在
在![]() 上的投影是
上的投影是![]()
![]() ,则
,则 ![]() ·
·![]() =
;
=
;
12. 已知两点A(3,-4)和B(-9,2),在直线AB上求一点P,使![]() =
=![]()
![]() ,则点P的坐标为
;
,则点P的坐标为
;
13. 已知点A、B、C三点共线,且![]() =
=![]()
![]() ,若
,若![]() =
=![]()
![]() ,则
,则![]() =
;
=
;
14. 已知点A(-2,2)、B(6,-4)、C(8,y)三点共线,则C分有向线段![]() 成的比
成的比
![]() =
,y=
;
=
,y=
;
15. 三角形ABC的三边中点分别为(2,1)、(-3,4)、(-1,-1),则其重心坐标为 ;
16. 在三角形ABC中,设A(3,7)、B(-2,5),若AC、BC的中点都在坐标轴上,则C点的坐标是 ;
17. 18. 已知![]() =(-1,3),
=(-1,3),![]() =(2,-1),若(k
=(2,-1),若(k![]() +
+ ![]() )⊥(
)⊥(![]() -2
-2![]() ),则k=
;
),则k=
;
18. 将函数y=x2-4x-1的顶点P按![]() 平移后得到P`(-1,3),则
平移后得到P`(-1,3),则![]() = ;
= ;
19. 将一抛物线F按![]() =(-1,3)平移后,得到抛物线F`的函数解析式为y=2(x+1)2+3,则F的解析式为
;
=(-1,3)平移后,得到抛物线F`的函数解析式为y=2(x+1)2+3,则F的解析式为
;
20. ![]() ABC中,A(2,-1),B(3,2)、C(-3,-1),AD是BC边上的高,则D点坐标是
.
ABC中,A(2,-1),B(3,2)、C(-3,-1),AD是BC边上的高,则D点坐标是
.
三. 解答题(15分×2=30分):
21.(1). 已知![]() =(-3,1),
=(-3,1),![]() =(0,5),若
=(0,5),若![]() ∥
∥![]() ,
,![]() ⊥
⊥![]() ,求
,求![]() .
.
(2). 已知![]() =(3,4),
=(3,4),![]() =(2,-1),若(
=(2,-1),若(![]() +x
+x![]() )⊥(
)⊥(![]() -
-![]() ),求x.
),求x.
22. 已知平行四边形ABCD一个顶点坐标是A(-2,1),一组对边AB、CD的中点分别为M(3,0)、N(-1,-2),求平行四边形ABCD各顶点的坐标。