奇偶性、单调性综合

　§4.8奇偶性、单调性综合

班级　　　　 学号　　　　　  姓名　　　　　  

一、　　　　　　 课堂目标：

掌握函数奇偶性的定义的基础上，解决函数综合性的一些问题

二、　　　　　　 要点回顾：

若某个函数是奇函数（或偶函数），则其定义域必须是关于原点对称的

三、　　　　　　 目标训练：

1、  已知函数f(x)=ax²+bx+c　(a0)是偶函数，那么g(x)=ax³+bx²+cx是　　　　　　　　　　　　　　　 (　　)

A. 奇函数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B. 偶函数

C. 既奇又偶函数　　　　　　　　 　　　　　　　　　　　　　　　　　 D.非奇非偶函数

　　　 2、已知f(x)=ax²+bx+3a+b是偶函数，且其定义域为[a-1,2a]，则a=__________ ,b=_________

　　　 3 、已知y=f(x)是定义在R上的奇函数，当x0时，f(x)=x²-2x ,则f(x)在R上的表达式是　 (　　)

　　　　　　　A. y=x(x-2)　　　　　　　　　B. y=x(x-1)　　　　　　　　　　　　C. y=x(x-2)　　　　　　　　 D.y=x(x-2)

　　　 4、已知f(x)=x⁵+ax³+bx-8，且f(-2)=10，那么f(2)等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　)

　　　　　　　A. -26　　　　　　　　　　　　　B. -18　　　　　　　　　　　　　　　　 C. -10　　　　　　　　　　　　　D. 10

　　　 5、函数f(x)=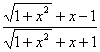是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　)

A. 奇函数　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　B. 偶函数

C. 既奇又偶函数　　　　　　　　　　　　　　　　　　　　　　　　　D.非奇非偶函数

　　　 6、设函数y=f(x) (xR且x0)对任意非零实数x₁,x₂均满足f(x₁x₂)=f(x₁)+f(x₂)，求证f(x)是偶函数。

　　　

7、若函数f(x)=，且f(2)=4.627，求f(-2)

　　　

8、已知f(x)=

(1)判断f(x)的奇偶性，(2)证明f(x)>0

　　　

9、求下列函数的单调减区间

　　　 （1）f(x)=sin(-x)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(2) f(x)=cos()

　　　

10、求y=的单调减区间

　　　

11、若函数y= a-bcosx的最大值为，最小值为，求y= 的最值