§5.３实数与向量的积（一）
班级 学号 姓名
一、课堂目标：（1）掌握实数与向量的积的定义，能说出实数与一个向量的积与这个向量的
模及方向之间的关系；
（2 ）掌握实数与向量的积的运算律，并会运用它们进行运算；
（3）理解两个向量共线的充要条件，会根据条件判断两个向量是否共线。
二、要点回顾：
1、实数与向量的乘积仍旧是一个 ，它的长度和方向规定如下：
（1）
=
（2）
时，
与
的方向 ；
时，与的方向 ；（3）
时，
，它的方向
。
2、实数与向量的积的运算律：设
为实数，、
为两个向量，则：
（1）
= ；（2）
= ；（3）
。
3、任一向量与非零向量共线的充要条件是
。
三、目标训练：
1、若AD是三角形ABC的中线，已知
，
，则
等于…………………（ ）
（A）
（B）
（C）
（D）
2、已知向量
、
不共线，若
3－４，
６+k，且∥，则k的值为（ ）
（A）8 （B）－８ （C）３ （D）－３
３、下面几组向量中共线的有
①2，2， ②－，－２+２
③４－
，－
④+，２－２（、不共线）
４、已知平行四边形ABCD中，
，若，
，则
等于…（ ）
（A）+
（B）－ （C）－
（D）－－
5、已知+，２－，则向量+2与2－…………………（ ）
（A）
一定共线（B）一定不共线（C）仅当与共线时共线（D）仅当=时共线
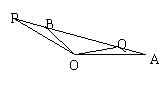6、如图（1）所示，已知
，
，用
，
表示
，则=…（ ）
（A）
（B）
|
（D）
7、若向量－2，２+，
6－２，且、不共线，
求证：
与
共线。
８、已知任意四边形ＡＢＣＤ中，Ｅ是ＡＤ的中点，Ｆ是ＢＣ的中点。
求证：
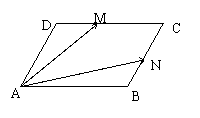９、如图（2）所示，平行四边形ABCD中，M、N分别为
DC、BC的中点，已知
，
，
|
、
表示
和。
10、在四边形ABCD中，
，
，
，
求证：ABCD为梯形
*11、如图（3）设平行四边形ABCD一边AB的四等分点最靠近B的一点为E，对角线BD
的五
|
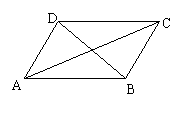等分点中靠近B的一点为F，求证：E、F、C三点在一条直线上