§5.3实数与向量的积（二）
班级 学号 姓名
一、课堂目标：了解平面向量的基本定理。
二、要点回顾：
1、 平面向量的基本定理：
如果
、
是同一平面内的两个不共线的向量，那么对该平面内的任一向量
，有且仅有一对实数
、
，使
，则、叫做
。
三、目标训练：
1、已知向量、不共线，实数
满足
+
=6+3，
则
的值等于…………………………………………………………………（ ）
（A）0 （B）2 （C）３ （D）－３
2、若
+与+共线，且、不共线，则实数的值等于……（ ）
（A）1 （B）－１ （C）
（D）以上都不对
３、P、Q分别为四边形ABCD的对角线AC、BD的中点。记
，
，则
=………………………………………………………………（ ）
（A）
+
（B）－+（C）－（D）－－
４、设，是两个不共线的向量，则向量2－与
+
（
）
共线的充要条件是……………………………………………………………（ ）
（A）=0 （B）=－１ （C）=－2 （D）=－
５、已知
＝，
＝，且
。∠ＡＯＢ＝
，又
，
且
平分∠ＡＯＢ，用，表示=
。
６、若
－+３，４+２，
－３+１２，
则向量写成
的形式是 。、
7、若
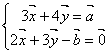，则
=
，
=
。
８、已知向量，不共线，实数满足等式
则x= y= 。
９、如图，已知梯形ABCD中，AB∥CD，且AB=2CD，M、N是DC、BA的中点，设
，
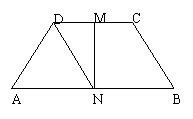
，试以、为基底表示
、
、
。
１０、在平行四边形ABCD中，点M是AB中点，点N在线段BD上，且有BN=
BD
求证：M、N、C三点在一条直线上。
1１、求证：始点相同的三个非零向量、、
的终点在同一条直线上
１２、如图，向量，，
有公共起点，且满足
（
），三个向量的终
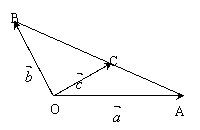点在同一条直线上，求证：