函数的单调性与奇偶性综合
班级 学号 姓名
一、基础练习：
1． 如果奇函数
在区间［3，7］上是增函数且最小值为5，那么在［-7，-3］上是
（ ）
A. 增函数且最小值为 -5 B. 增函数且最大值为 -5
C. 减函数且最小值为 -5 D. 减函数且最大值为 -5
2．函数
的单调递增区间是
.
3．已知
，当
，
时，为奇函数。
4．已知函数
若
，则 
=
。
5．已知函数是定义在 R上的奇函数，给出下列命题：
（1）．
；
（2）．若 在
[0, 
上有最小值 -1，则在
上有最大值1；
（3）．若 在
[1, 上为增函数，则在
上为减函数；
其中正确的序号是：
二、能力培养：
6．若y＝f(x)在区间(a，b)上是增函数，则下列结论正确的是 （ ）
B．y＝－f(x)在区间(a，b)上是减函数
C．y＝f(x)2在区间(a，b)上是增函数 D．y＝f(x)在区间(a，b)上是增函数
7．已知R上的函数是偶函数，在上单调递增，且对于
，
有
，则
（ ）
8． 已知
是R上的偶函数，且在
上是减函数，若
，则实数
的取值范围是
（ ）
A.
B. 
C. 
D. 
9．已知函数是定义在
上的奇函数，且
时，
，
（1）求的解析式； （2）求
的值。
10．已知：函数
在上是奇函数，而且在
上是增函数，
证明：在
上也是增函数。
三、综合拓展：
11．（1）定义在
上的奇函数为减函数，且
，求实数的取值范围。
(2) 定义在
上的偶函数
，当
时，为减函数，若
成立，求
的取值范围。
12．函数是定义在上的偶函数，在
上是减函数，且
，解不等式
参考答案
1．B 2. [-4, -1] 3. 
4. -26 5. (1) (2)
6. B 7. A 8. C
9. (1)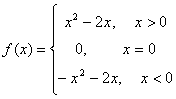
(2) 
10.略
11.
（1）甴条件得
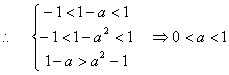
（2）甴条件得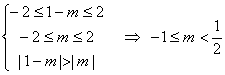
12. 甴得
∵函数是定义在上的偶函数，在上是减函数 ∴在
上为增函数
∴
∴
，或
或
∴不等式的解集为