《平面向量》单元测试题
班级 学号 姓名
一、选择题(请将正确答案的代号填入后面的答题卡内，每小题5分，共40分)
1． 若
＝(2,－1)，
＝(1,3)，则－2＋3＝
（ ）
(A)(－1,－11) (B)(－1,11) (C)(1,－11) (D)(1,11)
2．下列命题：
①∥Û存在唯一的实数l，使得＝l；
②∥Û存在不全为零的实数l1和l2，使得l1＋l2＝0；
③、不平行Û若l1＋l2＝0，则l1＝l2＝0；
④、不平行Û不存在实数l1和l2，使得l1＋l2＝0。
其中正确的命题是 （ ）
(A)①④ (B)②③ (C)①③ (D)②④
3．在平行四边形ABCD中，
＝ （ ）
(A)
(B)
(C)
(D)
4．已知P(3,－6)、Q(－5,2)、R(m,－9)三点共线，则实数m的值为 （ ）
(A)－9 (B)－6 (C)9 (D)6
5．已知＝
，＝2，·＝－3，则与的夹角为 （ ）
(A)150° (B)120° (C)60° (D)30°
6．下列命题中错误的是 （ ）
(A)
(B)l(·)＝·(l)
(C)(－)·
＝·－·
(D)∥Û·＝·
7．点P分
的比为
，Q为线段PM的中点，则N分
的比为 （ ）
(A)
(B)
(C)
(D)
8．已知向量
，
，
，，，满足++=0，若设
，
，
，则
为 （ ）
(A)等边三角形 (B)直角三角形 (C)等腰直角三角形 (D)等腰但不是等边三角形
二、填空题(每小题4分，共32分)
9．已知向量＝(2,－x)，＝(x,－8)的方向相反，则x＝ 。
10．点M(1,－2)关于点N(3,2)的对称点的坐标为 。
11．已知＝3，在上的射影为
，则·＝ 。
12．若＋＝(－1,－2)，－＝(3,4)，则＝ ，＝ 。
13．已知
＝3
1，
＝32，P、Q为线段AB的三等分点，则
＝ 。
14．已知＝(
,－3)，＝(2,l)，且⊥，则l＝ 。
15．ΔABC中，若∠A＝30°，a＝
，b＝2，则∠B＝ 。
16．如果向量与的夹角为θ，那么我们称×为向量与的“向量积”，×是一个向量，它的长度×＝sinθ，如果＝3，＝2，·＝－2，则×＝ 。
三、解答题(本大题共6个小题，满分78分)
17．在ΔABC中，已知b＝(－1)a，∠C＝30°，求∠A和∠B。 （12分）
18．用向量方法求等腰直角三角形中两直角边上的中线所成的钝角的度数。（12分）
 |
19．设
是与x轴、y轴方向相同的两个单位向量，
，
，求四边形ABCD的面积。（12分）
20．把函数
的图像
分别按下列向量平移：=（3，2）；=（0，—4）；=（1，—2），求平移后的图像
的解析式。由所得结论发现了什么规律？并总结出当向量满足什么条件时会发生这种现象。（12分）
 |
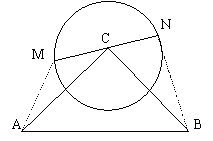21．.Rt△ABC中，∠C=900，AC=BC=2，⊙C的半径是1，MN是⊙C直径，
求：
·
的最大值及此时与
的关系。（14分）
22．已知向量＝(cos
,sin)，＝(cos
,－sin)，且x∈[0,
]。
(1)求·及＋；
(2)若f(x)＝·－l＋的最小值是－
，求l的值。（16分）