圆锥曲线综合（一）

圆锥曲线综合（一）

班级　　　　 学号　　　　　  姓名　　　　　  

一、　　　　　　 目标要点：

圆锥曲线的定义、方程及性质的灵活运用。

二、目标训练：

1．已知A(－1, 0), B(1, 0)，动点P满足PA+PB=2，则点P的轨迹方程是　　　　　　　 （　　　）

  （A）x²+y²=1　　　　（B）y=0 　　　 （C）y=0, x∈[－1, 1]　　 （D）

2．双曲线的两条渐近线的夹角是，则其离心率是　　　　　　　　　　　　　　　　  （　　　）

  （A）或2　　 （B）　　　　 （C）　　　　　　　 （D）不能确定

3．椭圆(1－m)x²－my²=1的长轴长是　　　　　　　　　 　　　　　　　　　　　　　　（　　 ）

（A）　 　 （B）　　 （C）　　　　（D）

4．椭圆的焦点是F₁和F₂，点P在椭圆上，若线段PF₁的中点在y轴上，则P F₁是P F₂的（　　）

  （A）7倍 　　　　（B）5倍　　　 （C）4倍　　　　（D）3倍

5．已知椭圆上有三个点A, B, C的横坐标成等差数列，则A, B, C三点到同一个焦点的距离成（　　　）

（A）等比数列　　（B）等差数列　（C）有时等差，有时等比 　（D）非等差等比数列

6．已知椭圆与双曲线有共同的焦点F₁(－4, 0), F₂(4, 0)，且椭圆的长轴长是双曲线的实轴长的2倍，则椭圆与双曲线的交点的轨迹方程是　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　　）

（A）(x±5)²+y²=9(y≠0)　　（B）(x±5)²+y²=9 　（C）x²+(y±5)²=9(x≠0)　　（D）x²+(y±5)²=9

7．设F₁, F₂是椭圆的两个焦点，P在椭圆上，已知P, F₁, F₂是一个Rt△的三个顶点，且

P F₁>P F₂，则P F₁ : P F₂的值是　　　　　　　　　　　　　　　　　　　　　　  （　　 ）

 （A）或2　　 （B）或　　　（C）或　　　（D）或2

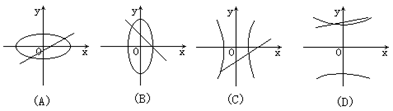
8．已知m,n为两个不相等的非零实数, 则方程mx－y+n=0与nx²+my²=mn所表示的示意曲线是(　 　 )

9．点P是椭圆=1上一点，F₁，F₂是其焦点，若∠F₁PF₂=60°,则ΔF₁PF₂的面积是　　 (　　 )

(A) 　　　 (B) 　　　　 (C) 20　　　　　(D)21

10*.方程表示的曲线是　　　　　　　　　 　　　　　　 (　　　 )

(A) 圆　　　　　 (B) 椭圆　　　　　 (C) 双曲线　　　　 (D) 抛物线

11．若抛物线y²=2px(p>0)上任一点Q到顶点O的距离与到焦点F的距离之比为k，则k的取值范围是　　　

12．点A(5, 3)，点P在抛物线y²=8x上移动，F为抛物线的焦点，当PA+PF取最小值时，点P的坐标是　　　　 。

13．若点A(1, 1), F₁是5x²+9y²=45的左焦点，点P是该椭圆上的动点，则PA+PF₁的最小值是　　　　　  。翰林汇

14．双曲线的渐近线方程是4x＋2y-3=0和2x-y＋6=0，则双曲线的离心率是　 　　　　。

15．命题：① 动点M到两定点A, B的距离之比为常数λ(λ>0且λ≠1)，则动点M的轨迹是圆；② 椭圆的离心率是；③双曲线的焦点到渐近线的距离是b；④已知抛物线y²=2px上两点A(x₁, y₁), B(x₂, y₂)，且OA⊥OB,(O是坐标原点)，则y₁y₂的值是－p². 上述命题中正确的是　　　　　　  。

16．电影放映机上的聚光灯泡的反射镜的轴截面是椭圆的一部分，灯丝在焦点F₂处，而且灯丝与反光镜的顶点A的距离F₂A=1.5cm，椭圆的通径BC=5.4cm，为了使电影机的片门获得最强的光线，灯泡应安在距片门多远的地方。

17．已知双曲线（a、b）的左、右两个焦点分别是F₁、F₂，P是它左支上一点，P到左准线距离为d.　(1)若是已知双曲线的一条渐近线，是否存在P点使d、PF₁、PF₂成等比数列？若存在，求出P点坐标；若不存在，说明理由；　(2)在已知双曲线的左支上，使d、PF₁、PF₂成等比数列的P点存在时，求离心率e的取值范围。