圆锥曲线综合（三）

圆锥曲线综合（三）

班级　　　　 学号　　　　　  姓名　　　　　  

一、　　　　　　 目标要点：

掌握直线与圆锥曲线问题常用方法。

二、　　　　　　 目标训练：

1．过P(1, 0)的直线l与抛物线y²=2x交于两点M, N，O为原点，若k_OM+k_ON=1，则直线l的方程是　（　　 ）

　（A）2x－y－1=0　（B）2x+y+1=0　（C）2x－y－2=0　（D）2x+y－2=0

2．若曲线y=ax²－1(a≠0)上有关于直线l: x+y=0对称的不同的两点A, B，则实数a的取值范围是　　(　　 )

　（A）a>　　　　（B）a<　　 （C）a>　　　　（D）a<

3．直线y=x+a与曲线x=－有且只有一个公共点，则a的取值范围是　　　　　　　  .

4．以抛物线y²=4x的焦点为圆心，且被抛物线的准线截得的弦长为2的圆的方程是　 　　　　　　　 。

5．直线y=x＋b与曲线(x＋2)²-3y²=81的交点为A、B，，则b=_________ 。

6．已知三条抛物线y=x²+4ax－4a+3, y=x²+(a－1)x+a², y=x²+2ax－2a中至少有一条与x轴有交点，则实数a的取值范围是 　　　　　　　　 。

7．过圆外一点P（3,2）引圆的两条切线，则经过两切点的直线方程是　　　　　　　　　 。

8．已知双曲线S的两条渐近线过坐标原点，且与以点为圆心，1为半径的圆相切，双曲线S的一个顶点与点关于直线对称。设直线过点，斜率为。
（1）求双曲线S的方程；　 （2）当时，若双曲线S的上支有且只有一个点到直线的距离为，求斜率的值及相应的点的坐标。

9．经过原点直线l与椭圆相交于A、B两点，若以AB为直径的圆恰好过椭圆左焦点F，求直线l的倾斜角．

9．已知双曲线方程为，过点P(－1, 0)作直线l交双曲线于A, B，问：使AB=3的直线l是否存在？若存在，求出方程；若不存在，说明理由。

10．已知某椭圆的焦点为，过点并且垂直于x轴的直线与椭圆的一个交点为，且。椭圆上不同的两点满足条件：、、成等差数列。
（1）求该椭圆的方程；（2）求弦AC中点的横坐标；（3）设弦AC的垂直平分线的方程为，求的取值范围。

11．已知抛物线C：，过点A（0，-2）的直线交抛物线于P、Q两点，以OP、OQ为邻边作平行四边形OPRQ。（1）求R点的轨迹方程；（2）是否存在直线，使四边形OPRQ为正方形，试证明你的结论。

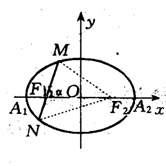12．如图所示，已知椭圆长轴A₁A₂=6,焦距F₁F₂=4,过焦点F₁作直线，交椭圆于两点M、N，设∠F₂F₁M=a(0£a<π), （1）当a取什么值时，MN等于椭圆短轴的长?（2）当a取什么值时，的面积最大，并求出最大值。