圆锥曲线综合（二）

圆锥曲线综合（二）

班级　　　　 学号　　　　　  姓名　　　　　  

一、目标要点：

掌握求曲线方程的常用方法：直接法、定义法、转移法、参数法等。

二、目标训练：

1.在直角坐标系中，和两坐标轴都相切的圆的圆心轨迹方程是　　　　　　　　　　　　　　 (　　　)

(A)y=x　　　 (B)y=x(x≠0)　　　 (C)x²-y²=0　　　 (D)x²-y²=0(x≠0)

2.如果点(a,b)在曲线y=x²+3x+1上,那么点(a+1,b+2)所在的曲线方程是　　　　　　　　　  (　　　)

(A)y=x²+5x+3　　 (B)y=x²+x-3　　 (C)y=x²+x+1　　 (D)y=x²-x+1

3．过椭圆内一点P(1, 0)作动弦AB，则AB的中点M的轨迹方程是　　　　　　  (　　　)

（A）4x²+9y²－4x=0　 （B）4x²+9y²+4x=0　（C）4x²+9y²－4y=0　　（D）4x²+9y²+4y=0

4．过点A(2, 1)的直线与双曲线2x²－y²=2交于P, Q两点，则线段PQ中点M的轨迹方程是　　(　　 )

（A）2x²－y²－4x+y=0　（B）2x²－y²+4x+y=0　（C）2x²－y²+4x－y=0　 （D）2x²－y²－4x－y=0

5．过抛物线y²=4x的顶点O的两弦OA, OB互相垂直，则AB中点M的轨迹方程是　　　　　 (　　 )

（A）y²=2x　　 （B）y²=2x+4　　（C）y²=2x－4　　 （D）y²=2(x－4)

6．已知点F(, 0)，直线l: x=－，点B是l上的动点，若过B垂直于y轴的直线与线段BF的垂直平分线相交于点M，则点M的轨迹是　　　　　　  　　　　　　　　　　　　　　　　　　　 （　　 ）

（A）双曲线　　　（B）椭圆 　　　（C）圆　　　　（D）抛物线

7．若将曲线y=f（x）向左平移，使原曲线上的点P（2，3）变为P′（1，3），则这时曲线的方程变为（ 　　）

(A) y=f(x)+1　　(B) y=f(x)-1　　(C) y=f(x+1)　　(D)y=f(x-1)

8．已知双曲线过坐标原点O，它的一个焦点是F(4, 0)，实轴长为2，则它的中心的轨迹方程是　(　　 )

（A）(x－2)²+y²=9 (x≠5)　　　　　　 （B）(x－2)²+y²=1 (x≠3)

（C）(x－2)²+y²=9或(x－2)²+y²=1　　 （D）(x－2)²+y²=9(x≠5)或(x－2)²+y²=1(x≠3)

9．过原点的椭圆的一个焦点为F(1, 0)，其长轴长为4，则另一个焦点的轨迹方程是　　　　　  (　　 )

（A）x²+y²=9　　　（B）x²+y²=9(x≠－3)　　 （C）x²+y²=9(x≠3) 　　 （D）x²+y²=9(x≠±3)

10．已知△ABC两顶点坐标分别为A(－2,0)、B(0,－2),第三个顶点C在曲线y=3x²－1上移动, 则△ABC重心的轨迹方程为_　　　　　　　  _______。

11．已知圆的方程x²＋y²＝25，点A为该圆上的动点，AB与x轴垂直，B为垂足，点P分有向线段的比λ=3/2．则点P的轨迹方程是　　　　　　　　　　　　 。

12．点P(－3, 0)是圆x²+y²－6x－55=0内一个定点，动圆M与已知圆相内切且过点P，则动圆M圆心的轨迹方程是　　　　　　　　　　　　 。

13．在四边形AOBP中，AOB=120⁰，AO^AP，BO^BP，AB=1，则(1)OP=__　　　___；(2)动点P 的轨迹方程是_____ ___　　　　 ____(以O为原点，AOB的平分线为y轴的正半轴建立直角坐标系)。

14．椭圆上有两点P、Q，若O为原点，斜率，则线段PQ中点M的轨迹方程是　　　　　　　　　　　　　 。

15．AB是圆O的直径，且AB=2a, M是圆上一动点，作MN^AB,垂足为N，在OM上取点P，使OP=MN，求点P的轨迹。

16．过双曲线C：的左焦点F作直线l与双曲线交于点P、Q，以OP、OQ为邻边作平行四边形OPMQ，求M的轨迹方程。

17．已知A, B是圆x²+y²=1上的动点，∠AOB=120°, C(a, 0)　(a≥0, a≠1)是定点，当点A在圆上运动时，指出△ABC外接圆圆心M的轨迹，并讨论方程表示的曲线类型与a的取值范围。

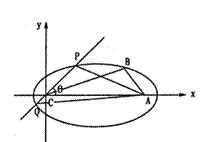18．在直角坐标系中，两个顶点C、A的坐标分别为（0，0）、，三个内角A、B、C满足.　

（I）求顶点B的轨迹方程；

（II）过顶点C作倾斜角为的直线与顶点B的轨迹交于P、Q两点，当 时，求面积 的最大值.