圆锥曲线综合（四）

圆锥曲线综合（四）

班级　　　　 学号　　　　　  姓名　　　　　  

一、　　　　　　 目标要点：

圆锥曲线中的常见最值问题。

二、　　　　　　 目标训练：

1．若实数x, y满足2x²－6x+y²=0，则x²+y²+2x的最大值是　　　　　　　　　　　　　 （　　　 ）

　（A）14　　　　 （B）15　　　　 （C）16　　　　　（D）17

2．曲线y²=4－2x上距坐标原点最近的点的坐标是　　　　　　　　　　　　　  　　　 （　　　 ）

  （A）(1, )　　 （B）(1, －)　　 （C）(1, ±)　　 （D）(±, 1)

3．已知F₁和F₂为椭圆的两个焦点，P为椭圆上一点，且∠F₁P F₂=60°,  则椭圆的离心率e的最小值为（　　）

  （A） 　　　（B）　　　 （C） 　　　　 （D）

4．双曲线的离心率为，双曲线的离心率为，则的最小值为（　　  ）

　　　　　　　　　　　　　　　　　　

5．已知点P在圆x²+(y－4)²=1上移动，点Q在椭圆上移动，则PQ的最大值是（　　　 ）

  （A）3　　　　（B）4　　　　 （C）5 　　　　　（D）6

6．已知A、B、C三点在曲线上，横坐标分别为1、m、4，则当的面积最大时，m等于 　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　）

7．定长为l(l>)的线段AB的端点在双曲线b²x²－a²y²=a²b²的右支上滑动，则AB的中点M的横坐标的最小值为　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　 ）

  （A）　（B）　（C）　（D）

8．抛物线y=x²上到2x－y=4距离最近的点的坐标是　　　　　　　　 。

9．若实数x, y满足(x－2)²+y²=1，则的取值范围是　　　　　　　　  ．

10．已知动点P在椭圆x²+a(y－1)²=a (0<a<1)上运动，则OP的最大值为　　　　　　　  。

11．已知椭圆(a>b>0)的长轴的两端点为A, B，如果C上存在一点P，使∠APB=120°，则C的离心率的取值范围是　　　　　　　  .

12．函数的最小值是　　　　　　　 。

13．点A(5, 3)，点P在抛物线x²=8y上移动，PN为P到x轴的距离，当PA+PN取最小值时，点P的坐标是　　　　　　　  .

14．若点A(1, 1), F₁是5x²+9y²=45的左焦点，点P是该椭圆上的动点，则PA—PF₁的最小值是　　　　　  。

15．椭圆有左焦点为F，过F点的直线l交椭圆于A、B两点，P为线段AB的中点，当的面积最大时，求直线l的方程。

16．在直线上任取一点P，过点P且以椭圆的焦点为焦点作椭圆。
（1）点P在何处时，所求椭圆的长轴最短；（2）求长轴最短时的椭圆方程。

17．如图，已知F(0, 1)，直线l: y=－2，圆C: x²+(y－3)²=1，

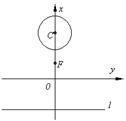（1）若动点M到点F的距离比它到直线l的距离小1，求动点M的轨迹E的方程；

（2）过轨迹E上一点P作圆C的切线，当四边形PACB的面积S最小时，求点P的坐标及S的最小值。

18、由椭圆的顶点引一条弦BP，求弦BP的最大长度。