三角函数知识整理
班级 学号 姓名
一、知识整理：
1．任意角的概念：正角： 负角： 零角： ；
象限角是指 ；轴线角是指 。
所有与角
终边相同的角（连同）组成的集合为
。
若是第一象限的角，则
是第
象限的角；若是第二象限的角，则是第 象限的角；
若是第三象限的角，则是第
象限的角；若是第四象限的角，则是第 象限的角；
2．弧度制:
,1
度；弧长公式
；扇形面积公式
3．任意角三角函数的定义:设是任意大小的角，
是终边上(除顶点外)的任意一点，点到原点
的距离为
，
则
；
；
；
；
；
；
4．用单位圆中的有向线段表示三角函数值：在下列图中分别画出各角的三角函数线：
=
=
=
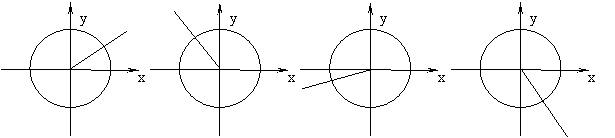
5．三角函数的符号、定义域和值域：
| 三角函数 | 定 义 域 和 值 域 | 三 角 函 数 的 符 号 | ||||
| 定 义 域 | 值 域 | 第一象限 | 第二象限 | 第三象限 | 第四象限 | |
|
| ||||||
|
| ||||||
|
| ||||||
6．同角三角函数的基本关系式：
（1）平方关系： 、 、 ；
（2）商数关系： 、 ；
（3）倒数关系： 、 、 。
7．诱导公式：
| sin | cos | tan |
| sin | cos | tan | |
| - |
| ||||||
|
|
| ||||||
|
|
| ||||||
| 2 |
| ||||||
|
|
| ||||||
-
+
记忆诱导公式的一句话是： 。
8．和差角公式：
①
②
③
④
9．两倍角公式：
=
=
=
升幂公式 降幂公式
=
=
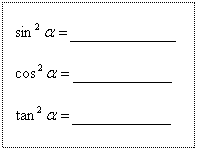
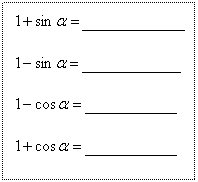10．归纳出一些角的常见变换形式：
如：
、
。
11．三角函数的合一变形：
（其中
由
确定）
如：
12．正弦、余弦、正切函数的图象与性质：
| 函数 | 正弦函数 | 余弦函数 | 正切函数 |
| 定义域 | |||
| 值域 | |||
| 最值及取最值时x的值 | |||
| 图象 | |||
| 对称轴 | |||
| 对称中心 | |||
| 周期性 | |||
| 奇偶性 | |||
| 单调性 |
13．正弦型函数：
（
）
（1）五点法画图时如何确定五个关键点：
（2）（）的图象可由
的图象通过怎样的变换得到？
方法一：
方法二：
（3）
（），
表示振动量时 ，振幅是 ，周期是
，
频率是 ，相位是 ，初相是 。
14． 叫实数a的反正弦。记作：
叫实数a的反余弦。记作：
叫实数a的反正切。记作：
二、补充练习
1、把函数
图象适当变换就可以得到
的图象，这种变换可以是（ ）
A、沿
轴方向向右平移
个单位
B、沿轴方向向左平移个单位
C、沿轴方向向右平移
个单位
D、沿轴方向向左平移个单位
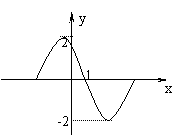2、右图是周期为
的三角函数
的图象，那么
可以写成（ ）
A、
B、
C、
D、
3、函数在同一周期内，当
时，
当
时，
则此函数的解析式为（ ）
A、
B、
C、
D、
4、函数
的图象关于原点中心对称的充要条件是（ ）
A、
B、
C、
D、
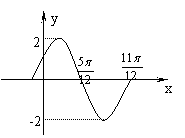5、已知右图是
的图象，则（
）
A、
B、
C、
D、
6、要得到
的图象，只须把
的图象向 平移
个单位。
7、函数
的图象的对称轴是
。
8、把函数
的图象向右平移
个单位，再将图上各点的横坐标压缩到原来的
，所得图象的解析式是
。
9、已知函数
的单调递减区间是
。
10、已知函数
，（1）求f(x)的单调递增区间;（2）若
，求f(x)的最大值和最小值