高一数学章节测试题（1-2）
第一章 集合与函数
时量 120分钟 总分 150分
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 如图，U是全集，M、P、S是U的三个子集，则阴影部分所表示的集合是
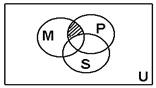A.（M
B.（M
C. （M
P）（
） D.（MP）
（）
2. 函数 
的值域是
A. 
B.
C. 
D.
3. 若偶函数
在
上是增函数，则
A．
B．
C．
D．
4. 函数
的单调递减区间为
A. 
B. 
C. 
D.
5. 下面的图象可表示函数y=f(x)的只可能是
y
y
y
y
 | |||||||
 | |||||||
 |  | ||||||
| |
0 x
0 x
0 x
0 x
A. B. C. D.
6. 函数
，满足
，则
的值为
A.
B. 8
C. 7
D. 2
7. 奇函数在区间[1，4]上为减函数，且有最小值2，则它在区间
上
A. 是减函数，有最大值
B. 是增函数，有最大值
C. 是减函数，有最小值
D. 是增函数，有最小值
 |
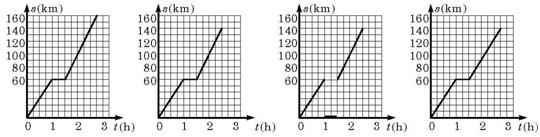8．(广东) 客车从甲地以60km／h的速度匀速行驶1小时到达乙地，在乙地停留了半小时，然后以80km／h的速度匀速行驶l小时到达丙地．下列描述客车从甲地出发，经过乙地，最后到达丙地所经过的路程s与时间t之间关系的图象中，正确的是
A. B. C. D.
9. 下列四个函数中，在（0，＋∞）上为增函数的是
A. f(x)=3－x B. f(x)=x2－3x C. f(x)=
D. f(x)=－︱x︱
10. 已知
，则f (x)
A. 是奇函数,而非偶函数 B. 是偶函数,而非奇函数
C. 既是奇函数又是偶函数 D. 是非奇非偶函数
选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题：本大题共5小题，每小题5分，共25分．把答案填在题中的横线上．
11. 如果一次函数的图象过点
及点
，则此一次函数的解析式为____________.
12. 若函数
的图象关于直线x=1对称，则b－a等于___.
13. 若函数y=ax与y=－
在R+上都是减函数，则y= ax2+bx+c在R+上是
（填“增”或“减”）函数。
14. 是定义域为R的奇函数，当
时，
，则
_________.
15. 设是
上的函数，且满足
，并且对于任意的实数x，y都有
成立，则
_____________.
三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．
16. （本小题共12分）
(1) 已知为全集，
，
，求
；
(2) 设集合
，
，若
，
求 
.
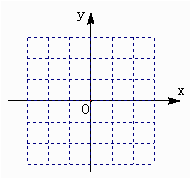
17.（本小题共13分）已知函数
.
（1）用分段函数的形式表示该函数；
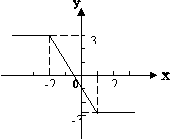
（2）在右边所给的坐标第中画出该函数的图象；
（3）写出该函数的定义域、值域、奇偶性、单调区间(不要求证明).
18.（本小题共13分）已知函数f ( x )=x 2+ax+b
（1）若对任意的实数x都有f (1+x)=f (1－x) 成立，求实数 a的值；
（2）若f (x)为偶函数，求实数a的值；
（3）若f (x)在[ 1，+∞)内递增，求实数a的范围。
19.（本小题共12分）某网民用电脑上因特网有两种方案可选：一是在家里上网，费用分为通讯费（即电话费）与网络维护费两部分。现有政策规定：通讯费为0.02元/分钟，但每月30元封顶（即超过30元则只需交30元），网络维护费1元/小时，但每月上网不超过10小时则要交10元；二是到附近网吧上网，价格为1.5元/小时。
（1）将该网民在某月内在家上网的费用y（元）表示为时间t（小时）的函数；
（2）试确定在何种情况下，该网民在家上网更便宜？
20. （本小题共12分）某企业为适应市场需求，准备投入资金20万元生产W和R型两种产品。经市场预测，生产W型产品所获利润
（万元）与投入资金
（万元）成正比例关系，且当投入资金为6万元时，可获利润1.2 万元。生产R型产品所获利润
（万元）与投入资金
（万元）满足关系
。为获得最大总利润，问生产W、R型产品各应投入资金多少万元？获得的最大总利润是多少？（精确到0.01万元）
21．（本小题共13分）已知定义在
上的函数同时满足下列三个条件：① 
;
② 对任意
都有
；③
.
（1）求
、
的值；
（2）证明：函数在上为减函数；
（3）解关于x的不等式
.
2007年高一数学章节测试题1.2（集合与函数）参考答案
一、选择题
1. C 2. C 3. D 4. C 5. D 6. B 7. A 8. B 9. C 10. A
二、填空题
11. y=－x+1 12. 10 13. 减 14.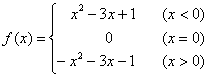
15. 
三、解答题
16. 解：（1）＝
;
（2）由已知得 a－3=－3 或2a－1=－3，得a=0或a=－1（舍）
所以 
.
17. 解：（1）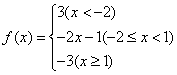
(2) 
（3）该函数的定义域为R.
该函数的值域为
.
该函数是非奇非偶函数.
该函数的单调区间为
.
18．解：（1） a=－2 (本小问5分）；
（2） a=0 (本小问4分）；（3）a ≥－2 (本小问4分，但求出a=－2只给1分）
19.解：（1）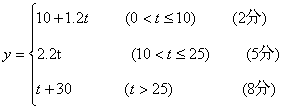
(2) 上网时间超过60小时则在家上网便宜。（12分）（没有过程适当扣分）
20．解：设生产R型产品投入资金为x万元，则生产W型产品的投入资金为（20－x）万元，所获总利润为y万元。
则由题可得：
令
, 则 
所以 
，即
（万元） ，y取最大值
（万元）
此时，20－x=10.23(万元)
答：（略） （答案未用小数表示及未答者分别扣1分）。
21. （1）解：
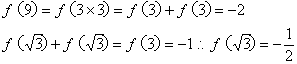
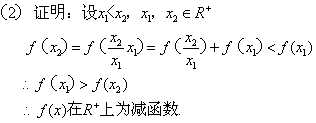
（3）不等式等价于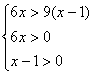
，解得 
.