高一数学上学期第一章试卷
本试卷分第I卷（选择题）和第II卷（非选择题）两部分。
第I卷1至2页。第II卷3至6页。共150分。考试时间120分钟。
第I卷（选择题60分）
一、选择题：本大题共12分,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1．下列各项中,不能组成集合的是（ ）
（A）所有的正数 （B）所有的老人
（C）不等于0的数 （D）我国古代四大发明
2．下列关系正确的是 （ ）
（A）
（B）
=
（C）
（D）
=
3．设集合A=｛2,3｝,B=｛2,3,4｝,C=｛3,4,5｝则
（ ）
（A）｛2,3,4｝ （B）｛2,3,5｝ （C）｛3,4,5｝ （D）｛2,3,4,5｝
4．设
＝{1,2,3,4} ,若
＝{2},(
A)∩B＝{4},(A)∩(B)={1},
则下列结论正确的是（ ）
（A）
且
（B）
且
（C）且
（D）且
5．下面说法正确的选项 （ ）
（A）函数的单调增区间只能有一个；
（B）函数的多个单调增区间的并集也是其单调增区间；
（C）具有奇偶性的函数的定义域定关于原点对称；
（D）关于原点对称的曲线一定是奇函数的图象.
6．下列各组函数中,表示同一函数的是 （ ）
（A）
（B）
（C）
（D）
7．在区间
上不是增函数的是（ ）
（A）
；（B）
；（C）
； （D）
.
8．函数
,
是（ ）
（A）奇函数 （B）偶函数 （C）不具有奇偶函数 （D）与
有关
9．如果奇函数在
具有最大值,那么该函数在
上 （ ）
（A）没有最小值 （B）没有最大值 （C）有最小值 （D）有最大值
10．已知
的定义域为
,则
的定义域为 （ ）
（A） （B）
（C）
（D）
11．已知函数
是R上的偶函数，且在(－∞,0]上是增函数，若
≥
,则a的取值范围是( )
（A）a≤2 （B）a≥－2 （C）a≤－2或a≥2 （D）－2≤a≤2
12．已知函数
若
则（ ）
（A）
（B）
（C）
（D）
与
的大小不能确定
二、填空题：(本大题共4小题,每小题4分,共16分。把答案填在题中横线上。)
13．若集合
,则
.
14．已知
,则
=
.
15．若函数
是偶函数,则的递减区间是
.
16．请写出符合下列条件的一个函数表达式 .
①函数在
上递减；②函数具有奇偶性；③函数有最小值3.
滕州高一上学期第一章试卷
第II卷（非选择题共90分）
注意事项：
1．第II卷共4页,用钢笔或圆珠笔直接答在试题卷中。
2．答卷前将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分数 | ||||||||
二、13、 14、 15、 16、
三、解答题（本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.）
17．（本小题满分12分）
（1）已知
,
,
,求
的值.
（2）已知
,
,
,求
的取值范围.
18．（本小题满分12分）设集合
,
,
,求实数的值.
19．（本小题满分12分）对于二次函数
，
①指出图像的开口方向、对称轴方程、顶点坐标；
②画出它的图像，说明其图像由
的图像经过怎样的平移得来；
③求函数的最大值或最小值；
④分析函数的单调性.
20．（本小题满分12分）已知是定义在
上不恒为0的函数,且对任意的
都满足
.
（1）求
、
的值. （2）判断的奇偶性,并证明你的结论.
21．（本小题满分12分） 分别指出函数
在
和
上的单调性,并证明之.
22．（本小题满分14分）在经济学中,函数的边际函数为
,定义为
,某服装公司每天最多生产100件.生产
件的收入函数为
（单位元）,其成本函数为
（单位元）,利润等于收入与成本之差.
（1）求出利润函数
及其边际利润函数
；
（2）分别求利润函数及其边际利润函数的最大值；
（3）你认为本题中边际利润函数最大值的实际意义是什么？
高一上学期9月数学竞赛试卷参考答案
一、选择题：（每小题5分,共60分）
1.B 2.C 3.D 4.B 5.C 6.A 7.B 8.A 9.C 10.D 11.D 12.B
二、填空题：（每小题4分,共16分）
13．5 14．0 15．
16．
或
（答案不唯一）
三、解答题：
17．解：（1）由已知得
.当
时,此时
,符合要求……………2分；
当
时,由
得
………………………………………………4分；
由
得
,所以的取值分别为0、1、2……………………………6分.
（2）当
时
,符合要求,此时
……………………8分；
当
时由题意得
解得m∈Φ,……………10分
所以的取值范围是
………………………………………………12分.
18．解：由及知 
……………4分,
解得或
…………………………………………………………………6分.
当时,
符合题意……………………………………………………9分；
当时,
不符合题意,舍去.故………………………………12分.
二次函数
19．解：①开口向下、对称轴方程为
、顶点坐标为(1,1); ……………3分
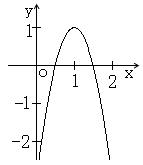②其图像由的图像向上平移1个单位和向右平移1个单位得来；………………………………………6分
③当时函数有最大值为1；………………9分
④函数的单调性：
在(－∞,1］上为增函数，在[1,+∞)上为减函数. ……12分
20．解：（1）由于对任意的 都满足,
令
得
………………………………………………2分；
令
得
,则
…………………………4分.
（2）是奇函数…………………………6分.
证明：由于对任意的 都满足 且,
令
,可以得到
………………………8分,
在中令
,
取任意实数
得
,所以是奇函数………………………12分.
21．解：
是增函数……………………………………2分
证明：任取
,不妨设x1
< x2,
则
……4分
由于
,所以
,
那么
是增函数……………………6分
（2）
是减函数…………………………………………8分,
证明：任取
,不妨设x1
< x2,
则…10分
由于
,所以
,
那么
是减函数……………………12分.
22．解：（1）
………3分
,
……………………………………………………………………6分.
（2）
,故当
62或63时,
7512（元）……………………………………………………9分.
因为
为减函数,当
时有最大值244……………………12分.
（3）当时边际利润函数取最大值,说明生产第二件衣服与生产第一件衣服的利润差最大…………………………………………………………………………14分.