高一数学上学期复习练习题
第一章 集合与函数概念
1.下列各项中,不可以组成集合的是 ( )
A.所有的正数 B.约等于2的数 C.接近于0的数 D.不等于0的偶数
2.已知集合![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.1 B.—1 C.1或—1 D.1或—1或0
3.以下四个关系:![]()
![]() ,
,![]()
![]() ,{
,{![]() }
}![]() ,
,![]()
![]()
![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A.1 B.2 C.3 D.4
4.下列四个集合中,是空集的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.设集合![]() ,
,![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]()
![]()
![]() C.
C.![]()
![]()
![]() D.
D.![]()
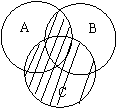 6.表示图形中的阴影部分( )
6.表示图形中的阴影部分( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.下面关于集合的表示正确的个数是 ( )
①![]() ; ②
; ②![]() ;
;
③![]() =
=![]() ;④
;④![]() ;
;
A.0 B.1 C.2 D.3
8.设全集![]() ,集合
,集合![]() ,集合
,集合![]() ,则 ( )
,则 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
9.已知![]() ,
,![]() ,且
,且![]() ,则a的值( )
,则a的值( )
A.1或2 B.2或4 C.2 D.1
10.设集合![]() ,
,![]() ,则
,则![]() .
.
11.已知集合![]() ,
,![]() ,
,![]() 那么集合
那么集合![]() ,
,![]() ,
,![]() .
.
12.下列各组函数中,表示同一函数的是 ( )
A.![]() B.
B.![]()
C .![]() D.
D. ![]()
13.已知函数![]() 的定义域为 ( )
的定义域为 ( )
A.![]() B.
B.![]()
C .![]() D.
D. ![]()
14.设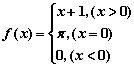 ,则
,则![]() ( )
( )
A.![]() B.0
C.
B.0
C.![]() D.
D.![]()
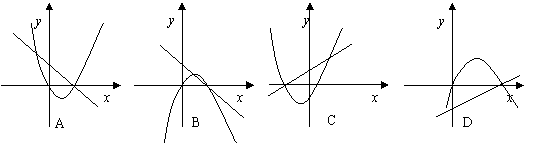
15.下列图中,画在同一坐标系中,函数![]() 与
与![]() 函数的图象只可能是 ( )
函数的图象只可能是 ( )
 |
16.设函数![]() ,则
,则![]() 的表达式为 ( )
的表达式为 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
17.在区间![]() 上为增函数的是 ( )
上为增函数的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
18. 函数![]()
![]() 是单调函数时,
是单调函数时,![]() 的取值范围 ( )
的取值范围 ( )
A.![]() B.
B.![]() C
.
C
.![]() D.
D. ![]()
19. 如果偶函数在![]() 具有最大值,那么该函数在
具有最大值,那么该函数在![]() 有 ( )
有 ( )
A.最大值 B.最小值 C .没有最大值 D. 没有最小值
20. 函数![]() ,
,![]() 是 ( )
是 ( )
A.偶函数 B.奇函数 C.不具有奇偶函数 D.与![]() 有关
有关
21. 函数![]() 在实数集上是增函数,则 ( )
在实数集上是增函数,则 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
22. 定义在R上的偶函数![]() ,满足
,满足![]() ,且在区间
,且在区间![]() 上为递增,则( )
上为递增,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
23. 设函数f (x)是(-![]() ,+
,+![]() )上的减函数,又若a
)上的减函数,又若a![]() R,则 ( )
R,则 ( )
A.f (a)>f (2a) B .f (a2)<f (a)
C .f (a2+a)<f (a) D.f (a2+1)<f (a)
24.已知![]() ,则
,则![]() =
.
=
.
25.函数![]() 在R上为奇函数,且
在R上为奇函数,且![]() ,则当
,则当![]() ,
,![]() .
.
26.函数![]() ,单调递减区间为
,最大值和最小值的情况为 .
,单调递减区间为
,最大值和最小值的情况为 .
27.设集合A={![]() },B={x
},B={x![]() },且A
},且A![]() B,则实数k的取值范围是
.
B,则实数k的取值范围是
.
28.若函数 f(x)=(K-2)x2+(K-1)x+3是偶函数,则f(x)的递减区间是 .
29.已知x![]() [0,1],则函数y=
[0,1],则函数y=![]() 的值域是
.
的值域是
.
30.已知![]() ,求函数
,求函数![]() 的单调递减区间并证明
的单调递减区间并证明
31.判断下列函数的奇偶性
①![]() ; ②
; ②![]() ;
;
③![]() ; ④
; ④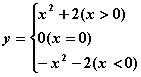
32.已知![]() ,
,![]() ,求
,求![]() .
.
30.已知f (x)是R上的偶函数,且在(0,+ ![]() )上单调递增,并且f (x)<0对一切
)上单调递增,并且f (x)<0对一切![]() 成立,试判断
成立,试判断![]() 在(-
在(-![]() ,0)上的单调性,并证明你的结论.
,0)上的单调性,并证明你的结论.
第二、三章
1.下列各式中成立的一项 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
2.函数![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.若指数函数![]() 在[-1,1]上的最大值与最小值的差是1,则底数a等于 ( )
在[-1,1]上的最大值与最小值的差是1,则底数a等于 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
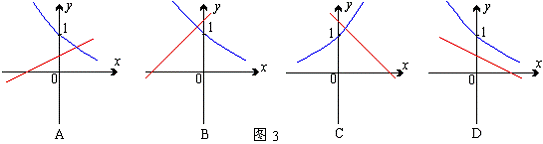
4.当![]() 时,函数
时,函数![]() 和
和![]() 的图象只可能是 ( )
的图象只可能是 ( )
5.函数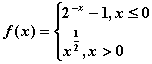 ,满足
,满足![]() 的
的![]() 的取值范围 ( )
的取值范围 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数![]() 的单调递增区间是 ( )
的单调递增区间是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知![]() ,则下列正确的是 ( )
,则下列正确的是 ( )
A.奇函数,在R上为增函数 B.偶函数,在R上为增函数
C.奇函数,在R上为减函数 D.偶函数,在R上为减函数
8.计算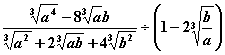 =
.
=
.
9.已知-1<a<0,则三个数![]() 由小到大的顺序是 .
由小到大的顺序是 .
10.对数式![]() 中,实数a的取值范围是 ( )
中,实数a的取值范围是 ( )
A.![]() B.(2,5) C.
B.(2,5) C.![]() D.
D. ![]()
11、函数![]() 的定义域为
( )
的定义域为
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12、设![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13、式子![]() 的值为 ( )
的值为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
14、如果lgx=lga+3lgb-5lgc,那么 ( )
A.x=a+3b-c B.![]() C.
C.![]() D.x=a+b3-c3
D.x=a+b3-c3
15、如果y=loga2-1x在(0,+∞)内是减函数,则a的取值范围是 ( )
A.|a|>1 B.|a|<2 C.a![]() D.
D.![]()
16、下列关系式中,成立的是 ( )
A.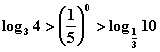 B.
B. 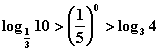
C. 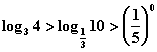 D.
D.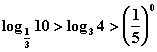
17、函数![]() 的定义域是 ,值域是 .
的定义域是 ,值域是 .
18、函数y=![]() 的单调递增区间是
.
的单调递增区间是
.
19、下列函数中既是偶函数又是![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
20、方程![]() 的解集是( )
的解集是( )
(A) {3} (B) {-1} (C) {-1,3} (D) {1,3}
21、下列函数:1y=![]() ; 2
; 2![]() 3y = x2; 4y= x -1;
3y = x2; 4y= x -1;
其中有2个零点的函数的序号是 。
22、根据表格中的数据,可以判定方程ex-x-2=0的一个根所在的区间为 ( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
A. (-1,0) B. (0,1) C. (1,2) D. (2,3)
23、设x,y,z∈R+,且3x=4y=6z.
(1)求证:![]() ; (2)比较3x,4y,6z的大小.
; (2)比较3x,4y,6z的大小.
24、已知函数![]() .
.
(Ⅰ)求函数的定义域;(Ⅱ)根据函数单调性的定义,证明函数![]() 是增函数.
是增函数.
25、设函数![]() , 求满足
, 求满足![]() =
=![]() 的x的值.
的x的值.
26、(1)已知![]() 是奇函数,求常数m的值;
是奇函数,求常数m的值;
(2)画出函数![]() 的图象,并利用图象回答:k为何值时,方程3X-1|=k无解?有一解?有两解?
的图象,并利用图象回答:k为何值时,方程3X-1|=k无解?有一解?有两解?
27、A、B两城相距100km,在两地之间距A城xkm处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数![]() .若A城供电量为20亿度/月,B城为10亿度/月.
.若A城供电量为20亿度/月,B城为10亿度/月.
(Ⅰ)把月供电总费用y表示成x的函数,并求定义域;
(Ⅱ)核电站建在距A城多远,才能使供电费用最小.