高一数学上学期空间几何体、点、线、面的位置关系复习
一、 选择题、
1、下列命题正确的是( )
A、有两个面平行,其余各面都是四边形的几何体叫棱柱。
B、有两个面平行,其余各面都是平形四边形的几何体叫棱柱。
C、有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱。
D、用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
2、利用斜二侧画法得到的①三角形的直观图是三角形 。②平行四边形的直观图是平行四边形。③正方形的直观图是正方形。④菱形的直观图是菱形。以上结论,正确的是( )
A、①② B、① C、③④ D、①②③④
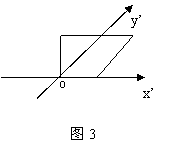
3、如图3所示为一平面图形的直观图,则此平面图形可能是图4中的( )
![]()
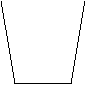

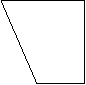
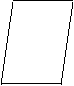
A B C D
图4
4、将一个长方体沿相邻三个面的对角线截出一个棱锥,则棱锥的体积与剩下的几何体体积的比为( )
A、1:2 B、1:3 C、1:4 D、1:5
5、若一个圆锥的轴截面是等边三角形,其面积为![]() ,则这个圆锥的全面积为( )
,则这个圆锥的全面积为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、一个漏斗形铁管接头,它的母线长是35CM,两底面直径分别是50CM和20CM,制作1万个这样的接头需要多少平方米的铁皮。(![]() 取3.1)( )
取3.1)( )
A、3798 B、2748 C、1099 D、1085
7、下列命题中,错误的是( )
A、平行于同一条直线的两个平面平行 B、平行于同一个平面的两个平面平行
C、一个平面与两个平行平面相交,交线平行
D、一条直线与两个平行平面中的一个相交,则必与另一个相交
8、若直线![]() 不平行于平面
不平行于平面![]() ,且
,且![]() ,则下列结论成立的是( )
,则下列结论成立的是( )
A、![]() 内的所有直线与
内的所有直线与![]() 异面
B、
异面
B、![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
C、![]() 内存在唯一的直线与
内存在唯一的直线与![]() 平行 D、
平行 D、![]() 内的直线与
内的直线与![]() 都相交
都相交
9、下列①若两条直线和第三条直线所成的角相等,则这两条直线互相平行。
②若两条直线都与第三条直线垂直,则这两条直线互相平行。
③若两条直线都与第三条直线平行,则这两条直线互相平行。
其中不正确的命题的个数是( )
A、0 B、1 C、2 D、3
10、平面![]() 与平面
与平面![]() 平行的条件可以是( )
平行的条件可以是( )
A、![]() 内有无穷多条直线都与
内有无穷多条直线都与![]() 平行
平行
B、直线![]() ,且直线
,且直线![]() 不在
不在![]() 内,也不在
内,也不在![]() 内
内
C、直线![]() D、
D、![]() 内的任何直线都与
内的任何直线都与![]() 平行
平行
11、下列命题正确的是( )
A、如果![]() 是两条直线,且
是两条直线,且![]() ,那么
,那么![]() 平行于经过
平行于经过![]() 的任何平面
的任何平面
B、如果直线![]() 和平面
和平面![]() 满足
满足![]() ,那么
,那么![]() 与
与![]() 内的任何直线平行
内的任何直线平行
C、如果直线![]() 和平面
和平面![]() 满足
满足![]() ,
,![]() ,那么
,那么![]()
D、如果直线![]() 和平面
和平面![]() 满足
满足![]() ,
,![]() ,
,![]() ,那么
,那么![]()
12、下列命题错误的是( )
A、如果![]() ,则
,则![]() 内所有的直线都垂直于
内所有的直线都垂直于![]()
B、如果![]() ,则
,则![]() 内一定存在直线平行于
内一定存在直线平行于![]()
C、如果![]() 不垂直于
不垂直于![]() ,那么
,那么![]() 内一定不存在直线垂直于
内一定不存在直线垂直于![]()
D、如果![]()
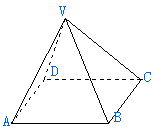 13、如图,四棱锥V—ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为
13、如图,四棱锥V—ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为![]() 的等腰三角形,则二面角V—AB—C的大小为( )
的等腰三角形,则二面角V—AB—C的大小为( )
A、![]() B、
B、![]() C、
C、![]() D、90
D、90![]()
二、 填空题、
1、圆台的上、下底面半径是![]() ,且侧面面积等于两底面面积之和,则圆台的母线长为
,且侧面面积等于两底面面积之和,则圆台的母线长为
2、圆半径扩大![]() 倍,其面积扩大 倍;球半径扩大
倍,其面积扩大 倍;球半径扩大![]() 倍,其表面积扩大 倍,体积扩
倍,其表面积扩大 倍,体积扩
大 倍。
3、已知长方体![]() 中,AB=
中,AB=![]() ,AD=
,AD=![]() ,
,![]() =2,则BC和
=2,则BC和![]() 所成角的大小为 ,
所成角的大小为 ,![]() 和
和![]() 所成角的大小为
。图:
所成角的大小为
。图:
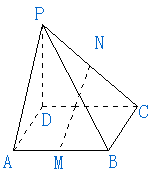 4、已知正四棱锥
4、已知正四棱锥![]() 如下图所示,底面面积为16,一条侧棱长为
如下图所示,底面面积为16,一条侧棱长为![]() ,
,
则高等于 ,斜高等于 。

(第4题) (第5题)
5、如上图,已知![]() 是矩形
是矩形![]() 所在平面外一点,
所在平面外一点,![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 中点。则
中点。则![]() 与平面
与平面![]() 的位置关系为
。
的位置关系为
。
三、 解答题、
1、已知空间四边形ABCD,AB=AC,DB=DC,求证:BC![]()
图:
2、如图,长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点。
的中点。
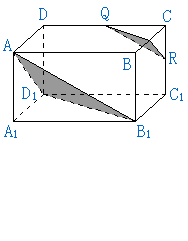 证明:平面
证明:平面![]() 与平面
与平面![]() 平行.
平行.
3、![]() 是等腰直角三角形,AC=BC=a,P是
是等腰直角三角形,AC=BC=a,P是![]() 所在平面外的一点,PA=PB=PC=
所在平面外的一点,PA=PB=PC=![]() ,(1)求证:平面PAB
,(1)求证:平面PAB![]() 平面ABC。(2)求PC与
平面ABC。(2)求PC与![]() 所在平面所成的角。
所在平面所成的角。
图:
4、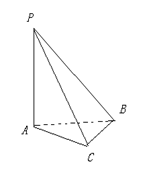 在三棱锥P-ABC中,
在三棱锥P-ABC中,![]() ,且AC=BC=5,PB=
,且AC=BC=5,PB=![]() ,求侧面PBC与底面ABC所成的二面角的大小。
,求侧面PBC与底面ABC所成的二面角的大小。