高一下学期数学期末综合测试
一.选择题：（本大题共12小题，每小题3分，共36分。在每题给出的四个选项中，只有一项是符合题目要求的。）
1．cos(－
)的值是
（A）
（B）－ （C）
（D）－
2．已知
=8，
为单位向量，当它们的夹角为
时，在方向上的投影为
（A）4
（B）4
（C）4
（D）8+
3．设cosα=-
,α∈（0, π）,则α的值可表示为
（A）arccos （B）-arccos （C）π-arccos （D）π+arccos
4．已知
=（5，-3），C（-1，3），
=2，则点D的坐标为
（A）（11，9） （B）（4，0） （C）（9，3） （D）（9，-3）
5．若
的值是
（A）2 （B）－2 （C） （D）
6．已知P1（-1，-6），P2（3，0），则点P（
，y）分有向线段
所成的比λ和y的值分别为
（A）
，-8 （B）
，8 （C），4 （D）
，-4
7．函数
的图象是
（A）关于原点成中心对称图形 （B）关于y轴成轴对称图形
（C）关于点（
，0）成中心对称图形 （D）关于直线x=成轴对称图形
8．在
则这个三角形的形状是
（A）锐角三角形 （B）钝角三角形
（C）直角三角形 （D）等腰三角形
9．函数要得到函数
的图像，只要把函数y=3sin2x 图像
（A）向右平移
个单位 （B）向左平移个单位
（C）向右平移
个单位
（D）向左平移个单位
10．已知A（1，2），B（4，2），则向量按向量（–1，3）平移后得到的向量是
（A）（3，0） （B）（3，5） （C）（–4，3） （D）（2，3）
11．下列各式中，值为的是
（A）sin150cos150 （B）
（C）
（D）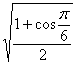
12．有四个函数①y=sin2x；②y=sinx；③y=sinx，④y=
,其中的周期T=π且在（0，
）上是增函数的个数是
（A）0 （B）1 （C）2 （D）3
二、填空题：（本大题共4小题，每小题3分 ，共12分。答案填在题中横线上。）
13．化简：
+
-
=____________．
14．在△ABC中，AC=,BC=,A=
,则AB的长为____________．
15．已知=3，
=2，与夹角为600，如果（3+5）⊥（m–），则m值为____________．
16．给出下列命题：
①存在实数x，使sinx＋cosx=
；
②若α、β是第一象限角，且α>β，则cosα<cosβ；
③函数y=sin(
x＋)是偶函数；
④函数y=sin2x的图象向左平移
个单位，得到函数y=sin(2x＋)的图象．
其中正确命题的序号是____________．（把正确命题的序号都填上）
三、解答题：（本大题共6小题，共52分，解答应写出文字说明，证明过程或演算步骤．）
17．（本题满分8分）
设两个非零向量
、
不共线，如果
=
+，
=2+8，
=3(-),求证A、B、D三点共线.
18．（本题满分8分）
已知函数
，且
．
（1）求a的值和
的最大值；
（2）问在什么区间上是减函数．
19．（本题满分8分）
已知=（1，2），=（-3，2），当k为何值时,
（1）k+与-3垂直;
（2）k+与-3平行？平行时它们是同向还是反向？
20．（本题满分8分）
航空测量组的飞机航线和山顶在同一铅直平面内，已知飞机的高度为海拔10000m,速度为180km（千米）/h（小时）飞机先看到山顶的俯角为150，经过420s（秒）后又看到山顶的俯角为450，求山顶的海拔高度（取＝1.4,＝1.7）．
|
21. （本题满分10分）
设平面内有四个向量
、
、
、
，且满足=-， =2-，⊥，==1．
(1)求，；
(2)若、的夹角为
，求cos.
22. （本题满分10分）
在△ABC中，a、b、c分别为角A、B、C的对边，已知
，c=
，又△ABC的面积为S△ABC=
，求a，b的值.
高一下学期数学期末综合测试
参考答案
一.选择题：
1.B, 2.A, 3.C, 4. D, 5. C, 6.A,
7.B, 8.B, 9.D, 10.A, 11.C, 12.B
二、填空题：
13.0, 14. ,
15. 
, 16 . ③.
以下的解答题只给出一种解法的评分标准，其它解法参照给分
三、解答题：
17．∵=+，=2+8，=3(-)
又 
＝+ …… 2分
＝2+8+3(-)
= 5(-) …… 4分
＝5 …… 5分
∴ 与 共线
…… 7分
∴即A,B,C 三点共线． …… 8分
18．⑴由于函数，
，
＝
∴a=1.
…… 2分
∴
∴的最大值是． …… 4分
⑵∵
依题意，当
，
…… 6分
∴ 
∴在区间 
，上为减函数． …… 8分
19．解：（1）k-＝（k+3，2k-2）
-3＝（10，-4）
……1分
∵k-与-3垂直
∴10（k+3）-4（2k-2）=0 ……3分
∴k=-19 ……4分
k=-19时k-与-3垂直．
（2）∵k-与-3平行
存在唯一实数
使k-＝（-3） ……5分
由（k+3，2k-2）＝（10，-4）
∴
解这个方程组得
＞０
……6分
∴ 
时, k-与-3平行；
＞０是同向． ……8分
20．解：如图
∵
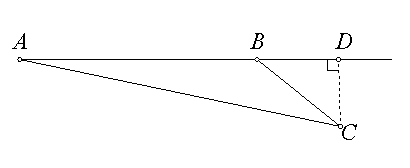
150 
450 ∴
300，
AB= 180km（千米）/h（小时）
420s（秒）=2100(m ) …… 2分
∴在
中
∴
…… 4分
∴
∵
，
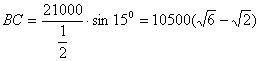
…… 6分
∴
＝
＝
＝
＝7350
山顶的海拔高度＝10000-7350=2650(米) …… 8分
21、解⑴∵=-， =2-
解得 ＝+，＝2+
…… 2分
∴
=(+)=+2+
∵⊥,∴=0,
…… 3分
∴=(+)=+2+=2, =
=(2+)=4+4+=5, =
…… 5分
⑵ 由cos=
∵=＝
．
∴
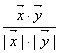
＝（+）（2+）＝2+3+=3 …… 8分
∴cos=
＝
．
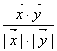…… 10分
22．解：∵在△ABC中,A+B+C=1800 ∴A+B =1800-C, …… 2分
又
得
∴
，
∴
，
∴
，∴∠C=600． …… 4分
由c=，得a2＋b2－2abcos600=()2 ①
由S△ABC=，得absin600= ② …… 6分
|
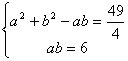
③＋④×3得
…… 8分
∴
，ab=6．
∴
，或
． …… 10分