数学“集合与函数概念”练习
一1．下面四个命题正确的是（ ）
A．10以内的质数集合是{0，3，5，7} B．“个子较高的人”不能构成集合
C．方程
的解集是{1，1} D．偶数集为
2．下面的结论正确的是（ ）
A．
，则
B．，则
{自然数}
C．
的解集是{-1，1} D．正偶数集是有限集
3．已知集合S={
}中的三个元素可构成
ABC的三条边长，那么ABC一定不是（ ） A．锐角三角形 B．直角三角形
C．钝角三角形 D．等腰三角形
4．设P=
，
，则
__________P。
5．0_______
6．1_________
。
7．设直线
上的点集为P，则P=____________。
点（2，7）与P的关系为（2，7）___________P。
8．集合
，用列举法可表示为_____________。
9．已知
，
，
，
，求
。
10．已知
，若集合P中恰有3个元素，求
。
11．已知集合M=
，若
，求满足条件的实数
组成的集合。
12．用适当的方法表示下图中的阴影部分的点（含边界上的点）组成的集合M。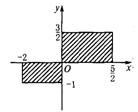
二1．下列四个命题：①＝
｛0｝；②空集没有子集；③任何一个集合必有两个或两个以上的子集；④空集是任何一个集合的子集．其中正确的有（ ）
A．0个 B．1个 C．2个 D．3个
2．集合｛1，2，3｝的子集共有（ ）A．7个 B．8个 C．6个 D．5个
3．若集合A＝｛x｜ax2＋2x＋a＝0，a∈R中有且只有一个元素，则a的取值集合是（ ）
A．｛1｝ B．｛－1｝ C．｛0，1｝ D．｛－1，0，1｝
4．集合A＝｛x｜x＝3k－2，k∈Z｝，B＝｛y｜y＝3l＋1，l∈Z｝，S＝｛y｜y＝6M＋1，
M∈Z｝之间的关系是（ ）
A．S＝B∩A
B．S＝B∪A C．S
B＝A D．S∩B＝A
5．已知集合A＝｛x｜－3≤x≤2｝，B＝｛x｜2m－1≤x≤2m＋1｝，且A
B，则实数m的取值范围是________．
6．已知A＝｛x｜x＜－1或x＞5｝，B＝｛x｜a＜x＜a＋4｝．若AB，则实数a的取值范围是________．
7．已知集合A＝｛x｜x2＋x－6＝0｝，B＝｛x｜ax＋1＝0｝，满足AB，则a能取的一切值是________．
8．若AB，AC，B＝｛0，1，2，3｝，C＝｛0，2，4，8｝，则满足上述条件的集合A为________．
9．已知集合M＝｛a，a＋d，a＋2d｝，P＝｛a，aq，aq2｝，其中a≠0，a、d、q∈R，且M＝P，求q的值．
10．已知集合A＝｛x｜ax2＋2x＋1＝0，a∈R，x∈R｝．
（1）若A中只有一个元素，求a的值，并求出这个元素；
（2）若A中至多只有一个元素，求a的取值范围．
三1．已知集合M、P、S，满足M∪P＝M∪S，则（ ）
A．P＝S B．M∩P＝M∩S
C．M∩（P∪S）＝M∩（P∩S） D．（S∪M）∩P＝（P∪M）∩S
2．已知M＝｛x2，2x－1，－x－1｝，N＝｛x2＋1，－3，x＋1｝，且M∩N＝｛0，－3｝，则x的值为（ ）A．－1 B．1 C．－2 D．2
3．设集合A＝｛（x，y）｜4x＋y＝6｝，B＝｛（x，y）｜3x＋2y＝7｝，则满足C
A∩B的集合C的个数是（ ）A．0 B．1 C．2 D．3
4．已知集合M＝｛x｜－1≤x＜2｝，N＝｛x｜x—a≤0｝，若M∩N≠，则a的取值范围是（ ）A．（－∞，2） B．（－1，＋∞） C．［－1，＋∞］
D．［－1，1］
5．已知集合A＝｛x｜y＝x2－2x－2，x∈R｝，B＝｛y｜y＝x2－2x＋2，x∈R｝，则
A∩B＝____．
6．满足｛x，y｝∪B＝｛x，y，z｝的集合B的个数是____．
7．已知集合A＝｛1，2，3，x｝，B＝｛3，x2｝，且A∪B＝｛1，2，3，x｝，则x的值为____．
8．设A＝｛x｜x2－2x－3＝0｝，B＝｛x｜ax－1＝0｝．若A∪B＝A，求实数a的值．
9． 50名学生参加体能和智能测验，已知体能优秀的有40人，智能优秀的有31人，两项都不优秀的有4人．问这种测验都优秀的有几人?
四1．下列各图中，可表示函数y＝f（x）的图象的只可能是（ ）
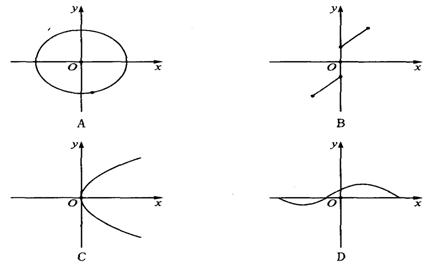
2．在下列四组函数中，f（x）与g（x）表示同一函数的是（ ）
A．f（x）＝x－1，g（x）＝
B．f（x）＝｜x＋1｜，g（x）＝
C．f（x）＝x＋1，x∈R，g（x）＝x＋1，x∈Z D．f（x）＝x，g（x）＝
3．国际上通常用恩格尔系数来衡量一个国家和地区人民生活水平的状况，它的计算公式，
n＝
（x：人均食品支出总额），且y＝2x＋475． 各种类型家庭：
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
| n | n≥59％ | 50％≤n＜59％ | 40％≤n＜50％ | 30％≤n＜40％ |
李先生的居住地2002年比1998年食品价格下降了7.5％，该家庭在2002年购买食品和1998年完全相同的情况下均少支出75元，则该家庭2002年属于……（ ）A．贫困 B．温饱 C．小康 D．富裕
4．拟定从甲地到乙地通话m分钟的电话费由f（m）＝1.06×（0.5·［m］＋1）（元）决定，其中m＞0，［m］是大于或等于m的最小整数，则从甲地到乙地通话时间为5.5分钟的电话费为（ ）A．3.71元 B．3.97元 C．4.24元 D．4.77元
5．已知f（x）＝
＋x＋1，则
＝______；f［］＝______．
6．已知函数f（x）＝
，那么
f（1）＋f（2）＋f（
）＋f（3）＋f（
）＋f（4）＋f（
）＝________．
7．求下列函数的定义域．
（1）
；
（2）
；
（3）
．
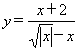8．求下列函数的值域．
（1）y＝－＋x＋2；
（2）y＝3－2x，x∈［－2，9］；
（3）y＝－2x－3，x∈（－1，2］；
（4）y＝
五1．设A＝｛x｜0≤x≤6｝，B＝｛y｜0≤y≤2｝，从A到B的对应法则f不是映射的是（ ）A．f：x→y＝x B．f：x→y＝x C．f：x→y＝x D．f：x→y＝
x
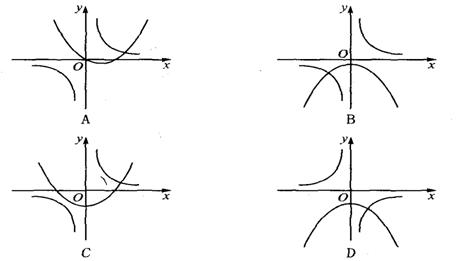
2．函数y＝ax2＋a与y＝
（a≠0）在同一坐标系中的图象可能是（ ）
3．设M＝｛x｜－2≤x≤2｝，N＝｛y｜0≤y≤2｝，函数f（x）的定义域为M，值域为N，则f（x）的图象可以是（ ）
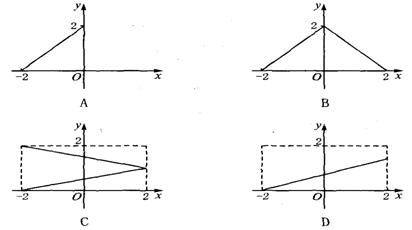
4．设函数f（x）＝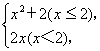
则f（－4）＝____，又知f（
）＝8，则＝____．
5．如图，有一块边长为a的正方形铁皮，将其四个角各截去一个边长为x的小正方形，然后折成一个无盖的盒子，写出体积V以x为自变量的函数式是_____，这个函数的定义域为_______．
6．给定映射f：（x，y）→（
，x＋y），在映射f下象（2，3）的原象是（a，b），则函数f（x）＝ax2＋bx的顶点坐标是________．
7．据报道，我国目前已成为世界上受荒漠化危害最严重的国家之一．图1表示我国土地沙化总面积在上个世纪五六十年代、七八十年代、九十年代的变化情况，由图中的相关信息，把上述有关年代中，我国年平均土地沙化面积在图2中表示出来．
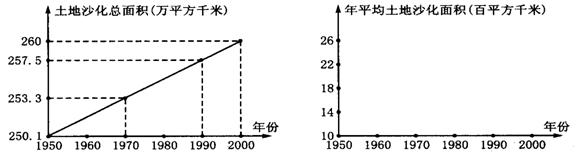
图1 图2
8．画出下列函数的图象．
（1）y＝x2－2，x∈Z且｜x｜≤2；
（2）y＝－2x2＋3x，x∈（0，2］；
（3）y＝x｜2－x｜；
（4）
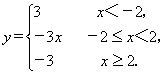
六1．函数y＝＝x2－6x＋10在区间（2，4）上是（ ）
A．递减函数 B．递增函数 C．先递减再递增 D．选递增再递减．
2．函数f（x）＝－x2＋2（a－1）x＋2在（－∞，4）上是增函数，则a的范围是（ ）
A．a≥5 B．a≥3 C．a≤3 D．a≤－5
3．函数y＝
的单调区间为___________．
4．函数f（x）＝2x2－3｜x｜的单调减区间是___________．
5．确定函数y＝x＋
（x＞0）的单调区间，并用定义证明．
6．快艇和轮船分别从A地和C地同时开出，如右图，各沿箭头方向航行，快艇和轮船的速度分别是45千米/时和15千米/时，已知AC＝150千米，经过多少时间后，快艇和轮船之间的距离最短？
7．设f（x）是定义在R上的增函数，f（xy）＝f（x）＋f（y），f（3）＝1，
求解不等式f（x）＋f（x－2）＞1．
七1．y＝f（x）（x∈R）是奇函数，则它的图象必经过点（ ）
A．（－a，－f（－a）） B．（a，－f（a）） C．（a，f（
）） D．（－a，－f（a））
2．设定义在R上的函数f（x）＝｜x｜，则f（x）（ ）
A．既是奇函数，又是增函数 B．既是偶函数，又是增函数
C．既是奇函数，又是减函数 D．既是偶函数，又是减函数
3．设f（x）是R上的偶函数，且在（0，＋∞）上是减函数，若x1＜0且x1＋x2＞0，则（ ）
A．f（－x1）＞f（－x2） B．f（－x1）＝f（－x2）
C．f（－x1）＜f（－x2） D．f（－x1）与f（－x2）大小不确定
4．已知f（x）＝x5＋ax3＋bx－8，f（－2）＝10，则f（2）=____．
5．若f（x）是偶函数，其定义域为R且在[0，＋∞）上是减函数，则f（－
）与
f（a2－a＋1）的大小关系是____．
6．已知函数f（x）＝x＋三，且f（1）＝2．（1）求m； （2）判断f（x）的奇偶性；
（3）函数f（x）在（1，＋∞）上是增函数还是减函数?并证明．
一1 B；2 C 3 D ；4 
；5 ；6 ；7 
，
；8 {9，10，11} ；9 为点（4，7）。
10 
；11 {－3，2}；12 
二1B；2B ；3D；4C ；5，－1≤M≤；6，a＞5或d≤－5 ；7，，－ ；8，，｛0｝，｛2｝，｛0，2｝；
9，q＝－；10（1）a＝0，x＝－或a＝1，x＝－1；（2）a≥1或a＝0．
三1D；2A；3C
；4C；5｛y｜－3≤y≤3｝；6，4；7，－1，0，±
；8，a的值为0，，－1．9，25人．
四1D ；2；B；3D；4C；5， 3＋，57；6，
；7（1）（－1，1）∪（1，2）；（2）R；（3）（－∞，0）．8，（1）（－∞，
）；（2）［－15，7］；（3）［－4，0］；（4）（－4，＋∞）．
五1A ；2D ；3B ；5，18，4或－
，；5，V＝
，｛x｜0＜x＜a/2｝；6，（
，－
）；
7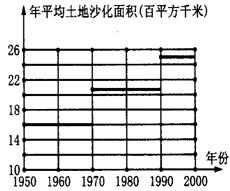
8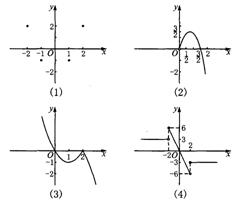
六1C ；2A；3，（－∞，－1），（－1，＋∞）；4，［0，］，（－∞，－）；5，增区间（1，＋∞），减区间（0，1）；6，3小时；7，x＞3或x＜－1． 七1D；2B ；3A ；4，－26 ；5，f（a2一a+1）≤f（）
6解：（1）f（1）：1＋m＝2，m＝1．
（2）f（x）＝x＋，f（－x）＝－x－＝－f（x），∴f（x）是奇函数．
（3）设x1、x2是（1，＋∞）上的任意两个实数，且x1＜x2，则f（x1）－f（x2）＝x1＋
－（x2＋
）＝x1－x2＋（－） ＝x1－x2－
＝（x1－x2）
．
当1＜x1＜x2时，x1x2＞1，x1x2－1＞0，从而f（x1）－f（x2）＜0，即f（x1）＜f（x2）．
∴函数f（x）＝＋x在（1，＋∞）上为增函数．