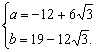正、余弦函数的图象和性质检测题
总分150分
一、选择题(每小题5分,共50分,请将正确答案填在题后的括号内)
1.函数![]() 的图象 ( )
的图象 ( )
A.关于原点对称 B.关于点(-![]() ,0)对称
,0)对称
C.关于y轴对称 D.关于直线x=![]() 对称
对称
2.函数![]() 为增函数的区间是 ( )
为增函数的区间是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.设a为常数,且![]() ,则函数
,则函数![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.函数![]() 的图象的一条对称轴方程是 ( )
的图象的一条对称轴方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 5.若函数
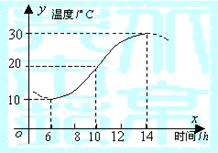
5.若函数![]() 的图象(部分)如图所示,则
的图象(部分)如图所示,则![]() 的取值是 ( )
的取值是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.下列函数中,以π为周期的偶函数是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如果函数y=sin2x+αcos2x的图象关于直线x=-![]() 对称,那么α的值为 ( )
对称,那么α的值为 ( )
A.![]() B.-
B.-![]() C.1 D.-1
C.1 D.-1
8.函数y=2cos2x+1(x∈R)的最小正周期为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知函数![]() ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )
A.![]() 是周期为1的奇函数 B.
是周期为1的奇函数 B.![]() 是周期为2的偶函数
是周期为2的偶函数
C.![]() 是周期为1的非奇非偶函数 D.
是周期为1的非奇非偶函数 D.![]() 是周期为2的非奇非偶函数
是周期为2的非奇非偶函数
10.函数![]() 的定义域是 ( )
的定义域是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(每小题5分,共25分,答案填在横线上)
11.已知函数![]() 的最小正周期为3
的最小正周期为3![]() ,则A=
.
,则A=
.
12.在0≤x≤![]() 条件下,则y=cos2x-sinxcosx-3sin2x的最大值为
条件下,则y=cos2x-sinxcosx-3sin2x的最大值为
13.已知方程![]() 有解,那么a的取值范围是
.
有解,那么a的取值范围是
.
14.函数y=![]() 的值域是__________
______________.
的值域是__________
______________.
15.定义在R上的函数![]() 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() 的值为
的值为
三、解答题(本大题共75分,16—19题每题12分,20题13分,21题14分)
16.已知函数![]()
(1)求![]() 的最小正周期;(2)求
的最小正周期;(2)求![]() 的单调区间;
的单调区间;
(3)求![]() 图象的对称轴,对称中心.
图象的对称轴,对称中心.
|
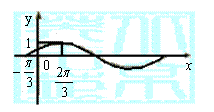
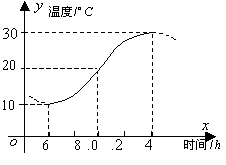
(Ⅰ)求这段时间的最大温差;
(Ⅱ)写出这段曲线的函数解析式.
18.已知函数y=sin2x+2sinxcosx+3cos2x. x∈R.
(1)求函数的最小正周期.
(2)函数的图象可由函数y=sin2x的图象经过怎样的变换得出?
19.已知函数y=a-bsin(4x-![]() )(b>0)的最大值是5,最小值是1,求a,b的值.
)(b>0)的最大值是5,最小值是1,求a,b的值.
20.函数f(x)=1―2acosx―2a―2sin2x的最小值为g(a),(a∈R).求:
(1)g(a);
(2)若g(a)=,求a及此时f(x)的最大值.
21.已知函数f(x)=2asin(2x-![]() )+b的定义域为[0,
)+b的定义域为[0,![]() ],值域为[-5,1],求a和b的值.
],值域为[-5,1],求a和b的值.
答案
一、选择题
1.B 2.C3.B 4.C 5.C6.A7.D 8.B 9.B10.C
二、填空题
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]() 15.-2≤y≤
15.-2≤y≤![]()
三、解答题
16.解析: (1)T=π;
(2)![]() 的单增区间,
的单增区间,
![]() 的单减区间;
的单减区间;
(3)对称轴为![]()
17. 解析:(Ⅰ)由图示知,这段时间的最大温差是
![]() (
(![]() )………2分
)………2分
(Ⅱ)图中从6时到14时的图象是函数![]() 的半个周期的图象,
的半个周期的图象,
∴![]() ,解得
,解得![]() ………5分
………5分
由图示,![]()
![]() ………7分
………7分
这时![]()
将![]() ,
,![]() 代入上式,可取
代入上式,可取![]() ………10分
………10分
综上,所求的解析式为
![]() ,
,![]() .………12分
.………12分
18.y=sin2x+cos2x+2=sin(2x+)+2.
(1)T=π,
(2)将y=sin2x的图象向左平移个长度单位,再向上平移2个单位长度即得.
19.解析: 由y=a-bsin(4x-![]() )的最大值是5,最小值是1及b>0知:
)的最大值是5,最小值是1及b>0知:
![]()
20.解:f(x)=2cos2x―2acosx―2a―1=2(cosx―)2――2a―1.
(1)当<-1即a<-2时.g(a)=1 . (此时cosx=-1).
当-1≤≤1即-2≤a≤2时.g(a)=――2a―1. (此时cosx=).
当a>2时,g(a)=2―2a―2a―1=1-4a. (此时cosx=1).
∴g(a)=.
(2)∵g(a)=1.显然a<-2和a>2不成立.
∴![]() a=-1或-3(舍).
a=-1或-3(舍).
∴f(x)=2cos2x+2cosx+1=2(cosx+)2+.
∴当cosx=1时,f(x)max=5.
21.解析: ∵0≤x≤![]() ,
,
∴-![]() ≤2x-
≤2x-![]() ≤π-
≤π-![]() =
=![]() π.
π.
∴-![]() ≤sin(2x-
≤sin(2x-![]() )≤1.
)≤1.
当a>0时,则![]() 解得
解得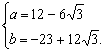
当a<0时,则![]() 解得
解得