高一数学上学期十八周周练
班别：高一（ ）班 姓名： 学号： 号
一．选择题
1．下列说法的正确的是 （ ）
A．经过定点
的直线都可以用方程
表示
B．经过定点
的直线都可以用方程
表示
C．不经过原点的直线都可以用方程
表示
D．经过任意两个不同的点
的直线都可以用方程
表示
2．直线
在
轴上的截距是 （ ）
A．
B．－
C． D．
3．经过点
的直线
到A
、B
两点的距离相等，则直线的方程为 （ ）
A．
B．
C．或 D．都不对
4．已知点
，点
在直线
上，若直线
垂直于直线
，
则点的坐标是 （ ）
A．
B．
C． D．
5．点
到直线
的距离为 （ ）
A．
B．
C．
D． 
6．若三条直线l1：x－y＝0；l2：x＋y－2＝0; l3：5x－ky－15＝0围成一个三角形，则k的取
值范围是 （ ）
A．k
R且k
5且k
1 B．kR且k5且k－10
C．kR且k1且k0 D．kR且k5
7．如果AC＜0且BC＜0，那么直线Ax＋By＋C＝0不通过 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
8．点M
与N
关于下列哪种图形对称 （ ）
A．直线 B．直线
C．点（
）D．直线
9．设A、B两点是
轴上的点，点
的横坐标为2，且
，若直线
的方程为
，则
的方程为 （ ）
A．
B．
C．
D．
10．直线kx－y＋1＝3k，当k变动时，所有直线都通过定点 （ ）
A．(0，0) B．(0，1) C．(3，1) D．(2，1)
11．在直线
到
距离最短的点是 （ ）
A．（0，0） B．（1，1） C．（－1，－1） D．（
）
12．直线l与两直线y＝1和x－y－7＝0分别交于A，B两点，若线段AB的中点为
M（1，－1），则直线l的斜率为 （ ）
A．
B．
C．－ D． －
二．填空体
13．若
，则
___ __．
14．若
，点
是
的垂直平分线上一点，则
___________．
15．若点
与点
的距离为5，则
．
16．当
= 时，直线
，直线
平行．
三．解答题
17．（12分）过点
作一直线l，使它与两坐标轴相交且与两轴所围成的三角形面积为5．
分析：直线l应满足的两个条件是
（1）直线l过点（－5, －4）；（2）直线l与两坐标轴相交且与两轴所围成的三角形面积为5.
如果设a，b分别表示l在x轴，y轴上的截距，则有
.
这样就有如下两种不同的解题思路：
第一，利用条件（1）设出直线l的方程（点斜式），利用条件（2）确定
；
第二，利用条件（2）设出直线l的方程（截距式），结合条件（1）确定a，b的值.
解法一：设直线l的方程为
分别令
，
得l在x轴，y轴上的截距为：
，
由条件（2）得
得
无实数解；或
，解得
故所求的直线方程为：
或
解法二：设l的方程为
，因为l经过点
，则有：
① 又
②
联立①、②，得方程组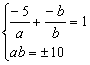
解得
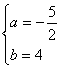或
因此，所求直线方程为：或.
18．（14分）已知两直线
,求分别满足下列条件的
、
的值．
（1）直线
过点
，并且直线与直线
垂直；
解：（1）
即
①
又点在上， 
②
由①②解得： 
（2）直线与直线平行，并且坐标原点到、的距离相等．
∥且的斜率为
. ∴的斜率也存在，即
，
.
故和的方程可分别表示为：
∵原点到和的距离相等. ∴
，解得：
或
.
因此
或
.
19．（12分）正方形中心在C（－1，0），一条边方程为：
，求其余三边直线
方程．
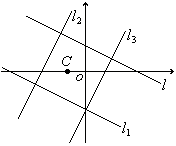解：设
为，的对边为
，的两邻边为
，
设的方程为：
，
∵C点到的距离等于C点到的距离；
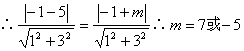
∴的方程为：
，
∵的斜率是
又∵
， ∴的斜率为3
设的方程为：
，即：
∵C到的距离等于C到l的距离. ∴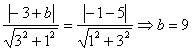
或
，
∴
的方程为：
，
的方程为：
20．（12分）已知直线l1：，l2：
，在两直线上方有一点P（如图），已知
P到l1，l2的距离分别为
与
，再过P分别作l1、l2的垂线，垂足为A、B，
|
（1）P点的坐标；
（2）AB的值．
略解（利用待定系数发设出P点的坐标即可）：
⑴点P（0，4）；
⑵AB=