高一数学周练(第8周)
1.集合的概念：
（1） 集合中元素特征，确定性，互异性，无序性；
（2） 集合的分类：
① 按元素个数分：有限集，无限集；
② 按元素特征分；数集，点集。
如:数集{yy=x2}，点集{(x，y)y=x2}
常用数集：N：自然数集或非负整数集；
：正整数集
Z：整数集；Q：有理数集；R：实数集
（3） 集合的表示法：
①列举法：用来表示有限集或具有显著规律的无限集，
如N+={1，2，3，…}；
②描述法。如:{xx>1}
2、两类关系：
（1）元素与集合的关系，用
或
表示；
（2）集合与集合的关系，用
，
,
，
,=表示，
需要注意的问题：注意概念间的区别和联系。如对“属于”与“包含”的理解：“属于”是指元素之间与集合之间的关系，“包含”是指集合与集合之间的关系；“属于”是集合最基本的关系，其他关系都是由它定义出来的。
（3）当AB时，称A是B的子集；当AB时，称A是B的真子集。
集合A的子集个数:
, 真子集个数:
练习:
1. 用符号“
”, “
”填空
（1）
______
, 
______, 
______
（2）
（3）
2. 已知A={xx≤3
,x∈R},a=
,b=2
,则（ ）
A.a∈A且bA B.aA且b∈A
C.a∈A且b∈A D.aA且bA
3. 以下五个式子中，错误的个数是（ ）
（1）
（2）
（3）
（4）
（5）
A. 2个 B. 3个 C. 4个 D. 5个
4. 下列序号正确的个数的有（ ）
①
本校的全体老教师
， ②集合A=
，③
， ④所有绝对值很少的数，⑤
表示空集，⑥空集是任何集合的真子集，
A、0个 B、3个 C、4个 D、6个
5.已知集合A＝
－1，3，2
－1
，集合B＝3，
．若B
A，则实数＝
6. 已知
，集合
，若
,则实数
。
7. 已知：集合
，若
，则a的取值范围：
.
8.集合运算集合M={1，2，3，4，5}的子集是
A、15 B、16 C、31 D、32:
9.满足条件
M
的集合M的个数是（ ）
A、4 B、3 C、2 D、1
3、交，并，补集：
(1)、交集：由所有属于集合A且属于集合B的元素组成的集合，称为集合A、B的交集，记作：
交集的性质：（1）
；（2）
，（3）
；
（4）
(2)、并集：由所有属于集合A或属于集合B的元素所组成的集合，称为集合A、B的并集，记作：
并集的性质：（1）
；（2）
；（3）
（4）
(3)、补集：已知全集I，集合
，由I中所有不属于A的元素组成的集合，称为A在I中的补集，记作：
补集的性质：（1）
，（2）
，
练习:
1设全集U={a，b，c，d，e}，集合M={a，c，d}，集合N={b，d，e}，则Cu（M∪N）等于（ ）．
（A）φ （B）{d} （C）{a，c} （D）{a，b，c，e}
2．若U={1,2,3,4},M={1,2}, N={2,3}, 则CU(M∪N)= ( )
(A){1,2,3} (B) {4} (C) {1,3,4} (D) {2}
3.集合
=（ ）．
(A)
(B){1} (C){0,1,2}
(D){-1,0,1,2}
4.设S={1，2，3}，M={1，2}，N={1，3}，那么（CSM）∩（CSN）等于（ ）
A．
B．{1，3} C．{1}
D．{2，3}
5.已知集合M＝｛xx＜3｝，N＝｛xlog2x＞1｝，则M∩N＝
（A） （B）｛x0＜x＜3｝
（C）｛x1＜x＜3｝ （D）｛x2＜x＜3｝
6.若集合
，
，则
_____________．
7.设集合A=
，B=
，则A
B等于（ ）
(A) 
(B) 
(C)｛xx>－3｝ (D)
｛xx<1｝
8. 设
,则
等于……（ ）
A．
B．
C．
D．
9.设A={(x，y) y=－4x+6}，B={(x，y) y=5x－3}，则A∩B=
A．{1，2} B．{(1，2)} C．{x=1，y=2} D．(1，2)
10.已知集合
，若
，则
=
若
且
，则
。
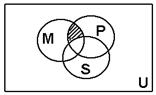11.如图，U是全集，M、P、S是U的三个子集，则阴影部分所表示的集合是（
）
（A）（M
（B）（M
（C）（MP）（CUS） （D）（MP）
（CUS）
指数与对数的运算
式子
值是______________；
将
化为分数指数幂的形式为
A.
B.
C.
D.
计算0.027
－(－
)－2+256
－3－1+(
－1)0=__________.
= 。
，
=___ __ .
方程
的解是
。
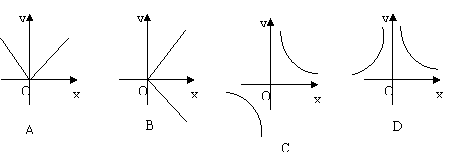
下列图象中不能作为函数y=f(x)的图象的是（ ）
已知函数f(x)=x2+ax+b满足f(1)=f(2)=0，则f(-1)的值是（ ）
A、-6 B、6 C、-5 D、5
已知
，则
=