高一数学第一学期第一阶段考试
数 学
（命题人：吕有红 2007.10.8）
（本试卷满分150分，考试时间120分钟）
一、选择题：(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.)
1、设
，
，则
等于 …………………（ ）
A. 
B. 
C. 
D. 
2、下列哪组中的两个函数是同一函数 ………………………………………… （ ）
（A）
与
（B）
与
（C）
与
（D）
与
3、已知集合A=
，B=
，则A∩B= （ ）
(A){(0，3)，(1，2)} (B){0，1} (C){3，2} (D){yy≤3}
4、设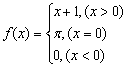
，则
…………………………………（ ）
A．
B．0
C．
D．
5、
（
）4（
）4等于 ………………………………… …………
（ ）
（A）a16 （B）a8 （C）a4 （D）a2
6、下列集合
到集合
的对应
是映射的是 …………………………………（ ）
（A）
：中的数平方；
（B）
：中的数开方；
（C）
：中的数取倒数；
（D）
：中的数取绝对值；
7、满足关系｛１，２｝
Ａ｛１，２，３，４，５｝的集合的个数是
……（ ）
A：4 B：6 C：8 D：9
8、设偶函数f(x)的定义域为R，当x
时f(x)是增函数，则f(-2),f(),f(-3)的大小关系是 ……………………………………………………………………………… （ ）
（A）f()>f(-3)>f(-2) （B）f()>f(-2)>f(-3)
（C）f()<f(-3)<f(-2) （D）f()<f(-2)<f(-3)
9、已知函数f（x）、g（x）定义在同一区间D上，f（x）是增函数，g（x）是减函数，且g（x）≠0,则在D上 ………………………………………………………… ( )
(A) f(x)+g(x)一定是减函数 （B）f(x)-g(x)一定是增函数
(C)f(x)·g(x)一定是增函数
(D) 
一定是减函数
10、下列函数式中，满足f(x+1)=
f(x)的是 ……………………………………
( )
(A) (x+1) (B)x+
(C)2x
(D)2- x
11、下列函数中，值域为（0，+∞）的是 ………………………………………… （ ）
（A）y=5
（B）y=(
)1-x （C）y=
（D）y=
12、F(x)=(1+
是偶函数，且f(x)不恒等于零，则f(x) …(
)
（A）是奇函数 （B）可能是奇函数，也可能是偶函数
（C）是偶函数 （D）不是奇函数，也不是偶函数
二．填空题：(本大题共7小题；每小题4分，共28分.)
13、已知
，
，则B＝
.
14、已知
,则
___________.
15、已知
，则
=
16、函数y =（）
的单调递减区间是
.
17、已知函数f(x)是定义在R上的奇函数,给出下列命题:
①f(0)=0;
②若f(x)在[0,+∞)上有最小值-1,则f(x)在(-∞,0)上有最大值1;
③若f(x)在[1, +∞)上为增函数,则f(x)在(-∞,-1)上为减函数;
④若x>0时, f(x)=x2-2x,则x<0时f(x)=- x2-2x.
其中正确的序号是: .
高一第一学期第一阶段考试 (10.8)
数 学（答卷纸）
二．填空题：(本大题共5小题；每小题4分，共20分.)
13、 14、
15、 16、
17、
三．解答题：（本大题共6小题，共70分．解答应写出文字说明、证明过程或推证过程．）
18、(10分)记函数f(x)=
的定义域为集合M，函数g(x)=
的定义域为集合N，求: (1)集合M、N； （2）集合M∩N，M∪N.
/
19(10分)、设集合
，
，
，求实数a的值.
20、（12分）设函数
．
1 求它的定义域；2 判断它的奇偶性；3
求证：
．
21、（12分）某市出租车的计价标准是：4公里以内10元，超过4公里且不超过18公里的部分1.2元/公里，超过18公里的部分1.8元/公里.
(1)如果不计等待时间的费用,建立车费与行车里程的函数关系式;
(2)如果某人乘车行驶了20公里,他要付多少车费?
22、（12分）已知函数f(x)是定义为（0，+∞）上的增函数，且满足f(xy)=f(x)+f(y)(x,y∈R+),f(2)=1.求：
(1)f(1); (2)满足f(x)+f(x-3)≦2的x的取值范围.
23、(14分)已知
（1）、当
时，求函数
的最大值和最小值.
（2）、求实数
的取值范围，使
在区间
上是单调函数.
（3）记f(x)的最小值为f(a)，求出f(a)的表达式，并求出f(a)的最大值.
答案
一、选择题：1、D 2、B 3、D 4、A 5、C 6、A 7、C 8、A
9、B 10、D 11、B 12、A
二、填空题：13、{0，1，2} 14、7 15、-1 16、（-∞，0） 17、①②④
三、解答题：
18、(1)M={x︱x<3/2},N={x︱x≦0}
(2)M∩N={x︱x≦0} M∪N={x︱x<3/2}
19、2
20、略
21、（1）当0≦x≦4时,y=10; 当4<x≦18时,y=1.2x+5.2;当x>18时,y=1.8x-5.6
(2) 当x=20时,y=30.4
22、(1)f(1)=0
(2)3<x≦4
23、（1）、f(x)最大=f(-5)=37；f(x)最小=f(1)=1
（2）、a≧5ora≦-5
(3) 当a>5,f(a)=27-10a; 当-5≦a≦5时, f(a)=2-a2;当a<-5时, f(a)=27+10a; f(a) 最大=2