高一数学模块测试题二(必修1)
考试时间:120分钟 满分100分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 下列关系中正确的个数为
① 0∈{0},② Φ![]() {0},③{0,1}
{0},③{0,1}![]() {(0,1)},④{(a,b)}={(b,a)}
{(0,1)},④{(a,b)}={(b,a)}
A. 1 B. 2 C. 3 D. 4
2. 下列对应中是集合A到集合B的映射的个数为
① A={1,3,5,7,9},B={2,4,6,8,10},对应法则f:x→y = x+1,x∈A,y∈B;
② A={xx是三角形![]() ,B={xx是圆
,B={xx是圆![]() ,对应法则f:每一个三角形都对应它的内切圆;
,对应法则f:每一个三角形都对应它的内切圆;
③ A={xx∈R},B={yy≥0},对应法则f:x→y = x2,x∈A,y∈B.
A. 0 B. 1 C. 2 D. 3
3.已知一次函数![]() 满足
满足![]() ,
,![]() ,则
,则![]() 解析式是
解析式是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 某林场计划第一年造林10000亩,以后每年比前一年多造林20%,则第四年造林
A. 14400亩 B. 172800亩 C. 17280亩 D. 20736亩
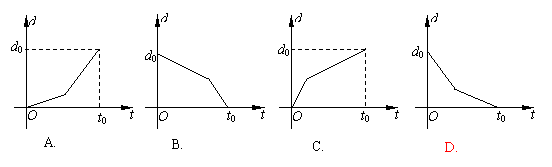
5. 某学生从家里去学校上学,骑自行车一段时间,因自行车爆胎,后来推车步行,下图中横轴表示出发后的时间,纵轴表示该生离学校的距离,则较符合该学生走法的图是
6. 已知函数![]() 在
在![]() 上单调递增,则实数
上单调递增,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. 函数![]() ,
,![]() 的值域是
的值域是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
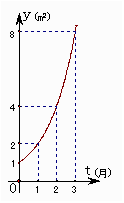
8. 如下图所示的是某池塘中的浮萍蔓延的面积y(m2)与时间t(月)的关系:y=at,有以下叙述:(1)这个指数的底数为2;(2)第五个月时,浮萍面积就会超过30m2;(3)浮萍每月增加的面积都相等; (4)若浮蔓延到2m2 ,3m2 ,6m2所经过的时间分别为t1,t2,t3,则t1+t2=t3 . 其中正确的有
 A. 1
B.
2
A. 1
B.
2
C. 3 D. 4
9. 函数![]() 在以下哪个区间内一定有零点
在以下哪个区间内一定有零点
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10. 如果二次函数f(x)=3x2+bx+1在(-∞,![]() 上是减函数,在
上是减函数,在![]() ,+∞)上是增函数,则f(x)的最小值为
,+∞)上是增函数,则f(x)的最小值为
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
选择题答题表
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中的横线上.
11. 若A={0,1,2,4,5,7,8},B={1,3,6,7,9},C={3,4,7,8},那么集合
(A![]() B)
B)![]() C =____________________.
C =____________________.
12. 函数![]() 的图象一定过定点P,则P点的坐标是
.
的图象一定过定点P,则P点的坐标是
.
13. a=log0.55,b=log0.53,c=log32,d=20.3,则a,b,c,d依小到大排列为 __<__<__<___.
14.设函数![]() 满足
满足![]() ,则
,则![]() .
.
15.定义在R上的奇函数![]() 为减函数,若
为减函数,若![]() ,给出下列不等式:
,给出下列不等式:
①![]() ;
②
;
②![]() ;
;
③![]() ;
④
;
④![]() .
.
其中正确的是 (把你认为正确的不等式的序号全写上).
三、解答题:本大题共6小题,共50分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分8分)
已知A={1,2,x2-5x+9},B={3,x2+ax+a},如果A={1,2,3},2 ∈B,求实数a的值.
17.(本小题满分8分)
(1) 已知![]() ,求
,求![]() 的值.
的值.
(2) 计算:![]()
18.(本小题满分8分)
证明: 判断函数![]() 在
在![]() 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
19.(本小题满分8分)对于函数![]() ,
,
(1)判断其奇偶性,并指出图象的对称性;
 (2)画此函数的图象,并指出其单调区间.
(2)画此函数的图象,并指出其单调区间.
20.(本小题满分9分)已知函数f(x) = x2
+mx – 4 在区间![]() 上的两个端点取得最大的最小值。
上的两个端点取得最大的最小值。
(1) 求m的取值范围;
(2) 试写出最大值y为m的函数关糸式;
(3) 最大值y是否存在最小值?若有,请求出来;若无,请说明理由.
21.(本小题满分9分) 商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少. 把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元. 现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
2007年高一数学模块测试题二(必修1)参考答案
一、选择题
B D A C D A D C B D
二、填空题
11.{1,3,4,7,8} 12. (1,4) 13. ![]() 14.
14. ![]() 15. ①④
15. ①④
三、解答题
16. 解:由A={1,2,x2-5x+9}={1,2,3},知x2-5x+9=3,解得x=2或x=3,
又2 ∈B,则x2+ax+a=2,当x=2时,a=![]() ,当x=3时,a=
,当x=3时,a=![]() .
.
故a=![]() 或
或![]() .
.
17. 解:(1)由![]() ,得
,得![]() ,
,
又![]()
∴![]()
由于![]() ,所以
,所以![]() .
.
(2)![]()
![]() .
.
18. 函数![]() 在
在![]() 上是增函数.
上是增函数.
证明:任取![]() ,且
,且![]() ,
,
则![]()
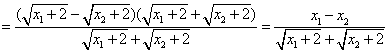
因为![]() ,得
,得![]()
所以函数![]() 在
在![]() 上是增函数
上是增函数
19. 解:(1)偶函数,图象关于y轴对称;
(2)图象略,增区间:![]() ;减区间:
;减区间:![]()
所以,商场要获取最大利润的75%,每件标价为250元或150元.
20. 解:(1) -![]()
![]() 或-
或-![]()
![]()
![]() 或m
或m![]() .
.
(2) 当m![]() 时,x=4时,最大值是y=4m+12;
时,x=4时,最大值是y=4m+12;
当m![]() , x=2时,最大值是y=2m
, x=2时,最大值是y=2m
∴ ![]() .
.
(3) 当m![]() 且m=-4时有最小值是y=-4;当m
且m=-4时有最小值是y=-4;当m![]() 时,无最小值。
时,无最小值。
综上所述,m 在它的取值范围内没有最小值。
21. 解:(Ⅰ)设购买人数为n人,羊毛衫的标价为每件x元,利润为y元,
则![]()
![]()
∵k<0,∴x=200时,ymax= - 10000k,
即商场要获取最大利润,羊毛衫的标价应定为每件200元.
(Ⅱ)由题意得,k(x-100)(x- 300)=- 10000k·75%
![]()
![]()