高中一年级数学模块考试(必修1)
班级__________________ 姓名_______________ 考号_________________
一:选择题:
1:下列各组对象中不能成集合的是( )
A,高一(1)班的全体男生 B ,该校学生家长全体
C,李明的所有家人, D, 王明的好朋友
2,已知X={xx>-4},则
A,0![]() X B,{0}
X B,{0}![]() X C,
X C,![]() X
D,{0}
X
D,{0}![]() X
X
3:已知A![]() {1,2, ,4},且A中最多有一个偶数,这样的A集合有( )
{1,2, ,4},且A中最多有一个偶数,这样的A集合有( )
A,2 B,4, C,5 D,6
4:三个数70。3,0。37,,㏑0.3,的大小顺序是( )
A, 70。3,0。37,,㏑0.3, B, 70。3,,㏑0.3, 0。37
C, 0。37, , 70。3,,㏑0.3, D, ㏑0.3,, 70。3,0。37,
5:,如果二次函数y=5x2-nx-10在区间(-![]() 是减函数,则n的值是( )
是减函数,则n的值是( )
A,1, B,-1, C,10, D,-10
6:下列函数中在区间(1,2)上是增函数的是( )
A,Y=![]() B,Y=X2+2X+1,
C,Y=-2X, D,Y=-2X2
B,Y=X2+2X+1,
C,Y=-2X, D,Y=-2X2
7:函数Y=-3X4是()
A,偶函数, B,奇函数, C,既是奇函数又是偶函数, D ,非奇非偶函数,
8:函数f(x)=(a2-3a+3)ax是指数函数 ,则a的值是( )
A,a=1或a=2
B,a=1
C,a=2
D,a>0或a![]() 1
1
9:f(x)=㏑x+2x-5的零点一定位于以下的区间( )
A,(1,2) B,(2,3) C,(3,4) D,(4,5)
10:在区间(-2,2)上有零点且能用二分法求零点的是( )
A,Y=X2-2X-3 B,Y=X2-2X+1,
C,Y=X2-2X+3 D,Y=-X2+2X-3
11,某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程。在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
A, 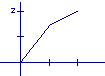 B
B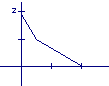
![]() C
C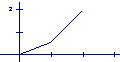 D
D 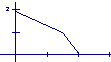
12:指数函数Y=ax在区间〔0,1〕上的最大值的和是3,则a=( )
A,1/2 B,4 C,2 D,-10
二:填空题:
![]() 13:计算㏒a1 +㏑e - 2
13:计算㏒a1 +㏑e - 2![]() =
=
![]() 14:函数y=
14:函数y=![]() 的定义域是
的定义域是
![]() 15:若f(x)为偶函数,当 X>0时,f(x)=x,则当x<0时,f(x)=
15:若f(x)为偶函数,当 X>0时,f(x)=x,则当x<0时,f(x)=
![]()
![]() 16:若指数函数f(x)与幂函数g(x)的图象相交于一点(2,4),则f(x)= ,g(x)=
16:若指数函数f(x)与幂函数g(x)的图象相交于一点(2,4),则f(x)= ,g(x)=
三:解答题:
17:设全集U为R,已知A={x1<x<7},B={xx<3或x>5},
求(1)A![]() B (2)A
B (2)A![]() B
(3)(CUA)
B
(3)(CUA)![]() (CUB)
(CUB)
18:已知f(x)=![]() ,证明f(x)在R上是奇函数。
,证明f(x)在R上是奇函数。
19:已知函数f(x)=![]() ,(x
,(x![]() 求这个函数的最大值和最小值
。
求这个函数的最大值和最小值
。
20:已知函数f(x)=㏒a![]() , (a>0且a
, (a>0且a![]() ,
,
求(1)函数的定义域。 (2)求使f(x)>0的x的取值范围。
21:经研究发现,学生的接受能力依赖于老师引入概念和描述总量所用的时间,开始讲题时,学生的兴趣保持较理想的状态,随后学生的注意力开始分散。分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力,x表示提出和讲授概念的时间(单位:分),有以下的公式:
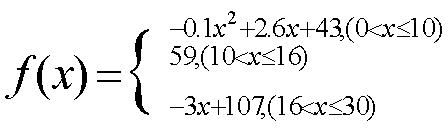
(1),开讲后5分钟与开讲后20分钟比较,学生的接受能力何时强呢?
(2),开讲后多少分钟,学生的接受能力最强?能维持多长的时间?
(3),若讲解这道数学题需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲完这道题?
参考答案:
一:D,D,D,A,C,.B,A,C,B,A,B,C.
二:(13)3/4;(14){xx![]() };(15)-x;(16)2x ,x2
};(15)-x;(16)2x ,x2
三:17:(1)R ; (2){x1<x<3或5<x<7}; (3){xx![]() }.
}.
18:证明:因为f-x)=![]()
![]() =-f(x),所以f(x)在R上是奇函数。
=-f(x),所以f(x)在R上是奇函数。
19:解:因为此函数在(1,+![]() 是减函数,所以在〔2,6〕是减函数,从而当x=2时有最大值2,当x=6时有最小值0。4
是减函数,所以在〔2,6〕是减函数,从而当x=2时有最大值2,当x=6时有最小值0。4
20:解:(1)![]() >0且2x-1
>0且2x-1![]()
(2)㏒a![]() >0,当a>1时,
>0,当a>1时,![]() >1
>1![]() 当0<a<1时,
当0<a<1时,![]() <1且x>0
<1且x>0![]()
21解:(1)f(5)=53.5
, f(20)=47![]() .开讲后5分钟学生的接受能力比开讲后20分钟强。
.开讲后5分钟学生的接受能力比开讲后20分钟强。
(2)当0<x![]()
f(10)=59;当16<x<30时,f(x)是递减的函数,![]() ,故开讲后10钟学生达到最强的接受能力,并维持6分钟。
,故开讲后10钟学生达到最强的接受能力,并维持6分钟。
(3)当0<x<10时,令f(x)>55,则6<x<10;当16<x<30时,令f(x)>55,则16<x<17.3
因此,学生达到或超过55的接受能力的时间11。3 分钟,小于13分钟,故这位老师不能在学生所需状态下讲完这道题。