高中一年级数学模块考试(必修3) 3
班级______________ 姓名____________ 考号______________
一. 选择题 (每小题4分,共48分)
1. 直线![]() (
(![]() 为实常数)的倾斜角的大小是( ).
为实常数)的倾斜角的大小是( ).
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
2. 到直线![]() 的距离为2的直线方程是( ).
的距离为2的直线方程是( ).
A. ![]() B.
B.
![]() 或
或![]()
C. ![]() D.
D.
![]() 或
或 ![]()
3. 下列说法正确的是( ).
A. 经过定点![]() (
(![]() ,
,![]() )的直线都可以用方程
)的直线都可以用方程![]() 表示.
表示.
B. 经过不同两点![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() )的直线都可以用方程
)的直线都可以用方程![]() 表示.
表示.
C. 经过定点![]() (0,
(0,![]() )且斜率存在的直线都可以用方程
)且斜率存在的直线都可以用方程![]() 表示.
表示.
D. 不过原点的直线都可以用方程![]() 表示.
表示.
4. 无论![]() 为何值,直线
为何值,直线![]() 总过一个定点,其中
总过一个定点,其中![]() ,该定点坐标为( ).
,该定点坐标为( ).
A.(1,![]() ) B.(
) B.(![]() ,
,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )
)
5. 若直线![]() :
:![]() 与
与![]() :
:![]() 平行,则
平行,则![]() 的值为( ).
的值为( ).
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
6. 一条直线与一个平面内的( )都垂直,则该直线与此平面垂直.
A. 无数条直线 B. 两条直线 C. 两条平行直线 D.两条相交直线
7. 下列四个命题中错误的个数是( ).
① 垂直于同一条直线的两条直线相互平行
② 垂直于同一个平面的两条直线相互平行
③ 垂直于同一条直线的两个平面相互平行
④ 垂直于同一个平面的两个平面相互垂直
A. 1 B. 2 C. 3 D. 4
8. 半径为![]() 的球内接一个正方体,则该正方体的体积是( ).
的球内接一个正方体,则该正方体的体积是( ).
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
9. 下列命题中错误的是( ).
A. 若![]() ,则
,则![]() B.
若
B.
若![]()
![]()
![]() ,
,![]()
![]()
![]() ,则
,则![]()
![]()
![]()
C. 若![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,则
,则![]()
![]()
![]()
D. 若![]()
![]()
![]() ,
,![]()
![]()
![]() =AB,
=AB,![]() //
//![]() ,
,![]()
![]() AB,则
AB,则![]()
![]()
![]()
10. ![]() 为
为![]() 所在平面外一点,
所在平面外一点,![]() ,
,![]() 在平面
在平面![]() 上的射影必在
上的射影必在![]() 的( ).
的( ).
A. ![]() 边的垂直平分线上 B.
边的垂直平分线上 B. ![]() 边的高线上
边的高线上
C. ![]() 边的中线上
D.
边的中线上
D. ![]() 的角平分线上
的角平分线上
11. 圆![]() :
:![]() 与圆
与圆![]()
![]() 的位置关系是( ).
的位置关系是( ).
A. 相交 B. 外切 C. 内切 D. 相离
12. 直线![]() 与圆
与圆![]() 相切,则
相切,则![]() 的值为( ).
的值为( ).
A. 1,![]() B.
B. ![]() C.
C.
![]() D.
1
D.
1
二. 填空题(每小题4分,共20分)
13. 圆![]() 截直线
截直线![]() 所得的弦长为__________,
所得的弦长为__________,
14. 过点(1,2)且与直线![]() 平行的直线的方程是
______________.
平行的直线的方程是
______________.
 15. 过点
15. 过点![]() (0,
(0,![]() ),
),![]() (2,0)的直线的方程为 ________.
(2,0)的直线的方程为 ________.
16. 已知各面均为等边三角形的四面体的棱长
为2,则它的表面积是____________.
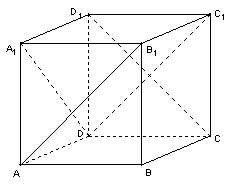
17. 如图,在正方体![]() 中,异面
中,异面
直线![]() 与
与![]() 所成的角为_______度;直线
所成的角为_______度;直线
![]() 与平面
与平面![]() 所成的角为_______度.
所成的角为_______度.
三. 解答题(第18、19题各9分,第20题14分,共32分)
18. 求经过两条直线![]() :
:![]() 与
与![]() :
:![]() 的交点
的交点![]() ,且垂直于直线
,且垂直于直线![]() :
:![]() 直线
直线![]() 的方程.
的方程.
19. 已知圆心为![]() 的圆经过点
的圆经过点![]() (0,
(0,![]() ),
),![]() (1,
(1,![]() ),且圆心在直线
),且圆心在直线![]() :
:![]() 上,求圆心为
上,求圆心为![]() 的圆的标准方程.
的圆的标准方程.
20. 如图:在三棱锥![]() 中,已知点
中,已知点![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 的中点.
的中点.
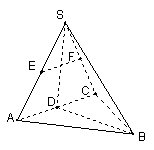 ①求证:
①求证:![]() ∥平面
∥平面![]() .
.
②若![]() ,
,![]() ,求证:平面
,求证:平面![]() ⊥平面
⊥平面![]() .
.
一、 选择题
DBCDA DBCBA AC
二. 填空题
13、![]() ;14、
;14、![]() ;15、
;15、![]() ;16、
;16、![]() ;17、
;17、![]() ,
,![]() .
.
三. 解答题
18、解:由![]() 解得
解得![]()
∴ 点P的坐标是(![]() ,2)
,2)
∵ 所求直线![]() 与
与![]() 垂直,
垂直,
∴ 设直线![]() 的方程为
的方程为 ![]()
把点P的坐标代入得 ![]() ,得
,得![]()
∴ 所求直线![]() 的方程为
的方程为 ![]()
19、 解:因为![]() (0,
(0,![]() ),
),![]() (1,
(1,![]() ),所以线段
),所以线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
直线![]() 的斜率
的斜率 ![]() ,
,
因此线段![]() 的垂直平分线
的垂直平分线![]() 的方程是
的方程是
![]() ,
,
即
![]()
圆心![]() 的坐标是方程组
的坐标是方程组 ![]() ,的解.
,的解.
解此方程组,得
![]() ,
,
所以圆心![]() 的坐标是(
的坐标是(![]() ,
,![]() ).
).
圆心为![]() 的圆的半径长
的圆的半径长
![]()
所以,圆心为![]() 的圆的标准方程是
的圆的标准方程是
![]()
10、解:①证明:∵![]() 是
是![]() 的中位线,
的中位线,
∴![]() ∥
∥![]() ,
,
又∵![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() .
.
②证明:∵![]() ,
,![]()
∴![]()
![]() ,
,
∵![]() ,
,![]()
∴![]()
![]() ,
,
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴平面![]() ⊥平面
⊥平面![]() .
.