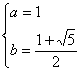|
|
学科：数学 |
| 教学内容：函数单元达纲检测（AA级） |
【同步达纲练习】
1.选择题(每小题3分)
1.给定映射f:(x、y)→(2x+y,xy)，(x、y∈R)的条件下，点(
，-)的原象是( )
A.(
，-
) B.(
，-
)或(-
，
)
C.(
，-) D.(
，-)或(-，)
2.下列各对应关系(其中x∈A，y∈B)：
①A=N,B=Z，f:x→y=2x-3
②A=｛1,2,3,4,5,6｝，B=｛y∈N｜y≤5｝，f:x→y=｜x-1｜
③A=｛x｜x≥1｝，B=｛y｜y=x2-2x+5｝，f:x→y=x2-2x+3
④A=N，B=｛y｜y=2x-1,x∈N｝，f:x→y=2x-1.
其中不是一一映射的( ).
A.只有① B.只有② C.只有③ D.只有①、③
3.函数y=(x+4)2在某区间上是减函数，这个区间可以是( )
A.(-∞，-4) B.［-4，+∞］ C.［4，+∞］ D.(-∞，4)
4.函数y=
(x∈R，且x≠
)的反函数是( )
A.y=(x∈R，且x≠) B.y=(x∈R,且x≠)
C.y=(x∈R,且x≠) D.y=(x∈R且x≠-2)
5.设函数f(x)=x2-bx+c f(0)=3.且f(1+x)=f(1-x),以下判断正确的是( )
A.f(bx)≤f(cx) B.f(bx)≥f(cx)
C.f(bx)＞f(cx) D.不能确定
6.函数y=2｜x｜的图像( )
A.关于y轴对称 B.关于x轴对称
C.关于原点对称 D.关于原点和坐标轴都不对称
7.若函数y=3+ax-1(a＞0，且a≠1)的反函数的图像恒过定点P，则P点的坐标为( )
A.(3，1) B.(3+a,2) C.(4,2) D.(4,1)
8.函数y=log
(4+3x-x2)的一个单调增区间是( )
A.(-∞，
) B.［，+∞］ C.(-1，) D.［，4)
9.已知方程(log3x)2-log3x2-2=0的两个根为α、β，则logαβ+logβα的值是( )
A.-4 B.-2 C.1 D.3
10.函数y=(a-1)x与y=(
)x具有不同的单调性，则M=(a-1)
与N=()3的大小关系是( )
A.M＜N B.M=N C.M＞N D.不能确定
11.给出某运动的速度曲线如图所示，试从以下的运动中选出一种，其速度变化最符合图中的曲线的是( )
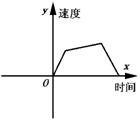
A.钓鱼 B.跳高 C.100米短跑 D.掷标枪
12.方程x+lgx=3,x+10x=3分别有根α、β，则α+β是( )
A.6 B.5 C.4 D.3
二、填空题(每小题4分)
13.设函数y=lg(x2-x-2)的定义域为A，函数y=
的定义域为B，则A∩B=
.
14.已知f(n)=
(n∈N)则f(5)=
15.已知f是从集合M到N的一一映射，其中M=｛a,b,c｝，N=｛-3，0，3｝，则满足f(a)+f(b)+f(c)=0的一一映射f的个数是 .
三、解答题(48分)
16.函数f(x)= +lg
.
(1)求此函数的定义域，并判断该函数的单调性；
(2)解关于x的不等式f［x(x-)］＜.
17.(1)求函数y=
(a＞0且a≠1)的定义域.
(2)已知f(x)的定义域为［0，1］，求函数y=f［log
(3-X)］的定义域.
18.1980年，我国人均收入255美元，若到2000年人民生活达到小康水平，即人均收入达到817美元，则年平均增长率是多少?若不低于此增长率递增，则到2010年人均收入至少多少美元?
19.某收购站分两个等级收购小麦，一等小麦每千克为a元，二等小麦每千克b(b＜a)元，现有一等品小麦x千克，二等品小麦y千克，若以两种价格的平均数收购，是否公平合理?
20.f(x)是定义在(-∞，10)∪［10，+∞］上的奇函数，且f(x)在［10，+∞］上单调递减.
(1)判断f(x)在(-∞，10］上单调性，并用定义证明之.
(2)对于a＞0且a≠1有f(-(ax+1)2-ax)+f(a2x-6ax+10)＞0.求x的取值范围.
21.y=f(x)是定义在R上的奇函数，当x≥0时，f(x)=2x-x2.
(1)求x＜0时，f(x)的解析式.
(2)问是否存在这样的正数a,b，当x∈［a,b］时，g(x)=f(x)，且g(x)的值域为［
,］?若存在，求出所有的a,b值，若不存在，请说明理由.
参考答案：
【同步达纲练习】
一、1.B 2.D 3.A 4.A 5.D 6.A 7.D 8.D 9.A 10.C 11.C 12.D
二、13.［-2，-1］ 14.8 15.6
三、16.解：(1)y=+lg
在(-1，1)上是减函数.
(2)0＜x＜
＜x＜0或＜x＜
17.解：因为1-loga(x+a)＞0所以loga(x+a)＜1.当a＞1时0＜x+a＜a所以函数的定义域为(-a,0)当0＜a＜1时，x+a＞a，所以函数的定义域为(0，+∞).(2)［2，
］.
18.年平均增长率为6％，到2010年人均收入至少是1464美元.
19.(1)若x＞y，则收购站受益；(2)若x＜y，则收购站吃亏；(3)若x=y，则两种收购方式付款额相等.
20.(1)f(x2)＜f(x1)即f(x)在(-∞，-10］上是减函数.
(2)已知-f［(ax+1)2+ax］＞-f(a2x-6ax+10)，因为(ax+1)2+ax＞0，a2x-6ax+10=(ax-3)2+1≥1.所以(ax+1)2+ax与a2x-6ax+10同属于f(x)的一个单调区间［10，+∞］，且要满足(ax+1)2+ax＞a2x-6ax+10≥10解得ax≥6 所以当0＜a＜1时，x≤loga6，当a＞1时，x≥loga6.
21.(1)设x＜0，则-x＞0，于是f(-x)=-2x-x2，又f(x)为奇函数，所以f(x)=-f(-x)=2x+x2 即x＜0时，f(x)=2x+x2(x＜0).
(2)