函数及其性质

函数及其性质

(1) 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

(2) 下列四组函数中，表示同一函数的是　　　　　　　　　　　　　　　　　（　）

A．　　　　　　　　  B．

C．　　　　　　　　　 　　 D．

(3) 函数的定义域为，那么其值域为　　　　　　　　　　（　）

A．　　　　 B．　　　　　  C．　　　　D．

(4) 设函数f(x) (x∈R)是以3为周期的奇函数, 且f(1)>1, f(2)= a, 则　　　　　 　　　　　(　　　)

　　　 A．　a>2　　　　 B．　a<-2　　　　　 C．　a>1　　　　  D．　a<-1

(5)设f(x)为奇函数, 且在(-∞, 0)内是减函数, f(-2)= 0, 则x f(x)<0的解集为　　 　　　 (　　　)

A．　(-1, 0)∪(2, +∞)　　 B．　 (-∞, -2)∪(0, 2 )　　 C． (-∞, -2)∪(2, +∞) 　D．　(-2, 0)∪(0, 2 )　

(6) 设函数的反函数定义域为 　　　　　　　　　　　　　(　　　)

　　　 A．　　　　  B．　　　　　　 C．（０，１）　　　　　  D．　

 (7) 下列各图象表示的函数中，存在反函数的只能是　　　　　　　　　　　　　（　）

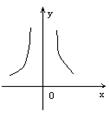
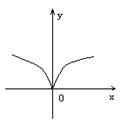
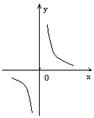
Ａ．　　　　　Ｂ．　　　　　　　Ｃ．　　　　　　Ｄ．　

(8)设函数f(x)=, 当x∈[-4, 0]时, 恒有f(x)≤g(x), 则a可能取的一个值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　A．　-5　　　　  B．　5　　　　　  C．　-　　　　　  D．　

(9) 已知函数f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y), 且f(2)=4,则f(-1)=　　　　　　　(　　　)

 A．　-2　　　 B．　1　　　　 C．　0.5　　　　  D．　2

(10) 已知，则下列不等式中成立的一个是　　　　　　　　　　　　　　（ ）

A．　　　　　  B．　　　　　　 C．　　　　  D．

 (11) 奇函数定义域是，则　　　　 .(12) 若，则＿＿(13) 函数在上的最大值与最小值之和为　　  .

(14) 在R上为减函数，则　　　　.

参考答案

1.B　2.D　 [解析]：∵=x -1∴A错

　　　 ∵的定义域是x1, 的定义域是x>1 ∴B错

∵的定义域是x>0 ,的定义域是x0 ∴C错

3.A　[解析]：只需把x=0，1，2，3代入计算y就可以了

4.D　 [解析]：

5.C  [解析]：

6.B[解析]：函数的反函数定义域

就是原函数的值域

而

当时原函数是是减函数，故

7. Ｄ　[解析]：根据反函数的定义，存在反函数的函数x、y是一一对应的。

8. A　 [解析]：排除法，

　　　　　　  若a=5,则x=0时f(x)=5，g(x)=1, 故A错

若a=,则x= - 4时f(x)= ，g(x)=, 故C错

若a=,则x=0时f(x)= ，g(x)=1, 故D错

9.A　 [解析]：因为函数f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y),所以 即 又

　　　　　　　 

10.D　　  [解析]：故

11. －１　　[解析]：∵是奇函数

∴定义域关于原点对称

即　　 ∴

12.－５　　　　[解析]：1 – 23= - 5

13.　  ３　　　 [解析]：函数在上是增函数，所以最大值为2，最小值为1，它们之和为3

14.[解析]：∵在R上为减函数　∴