高一数学期中测试题(一)

高一数学期中测试题(一)

本试卷分第Ⅰ卷(选择题　共60分)和第Ⅱ卷(非选择题　共90分),考试时间为120分钟,满分为150分.

第Ⅰ卷　(选择题　共60分)

一、选择题: 本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的.

1、若则 （　　）

A、 　　　　　 B、 　　　　 C、 　　　 D、

2、已知扇形的周长是6cm，面积是2cm²，则扇形的中心角是弧度数是　　　 （　　）

　A. 1　　　　　　  B. 4　　　　　　 C. 1或4　　　　　  D. 2或4

3、已知cos31°=m,则sin239°·tan149°的值是 　　　　　　　　 （　 ）

A.　　　　 B.　　　　　　C.　　　　　　　　　 D.-

4、设且在的延长线上，使,则点的坐标是

A、　　　B、 　　　C、　　　 D、

5、已知函数为奇函数，则的一个取值为（　　）

A、0　　　　　　 B、　　　　　  C、　　　　  D、

6、已知,且关于的方程有实根,则与的夹角的取值范围是　 (　　　)

A.[0,]　　　　 B.　　　　 C.　 　　 D.

7、函数是（　　）

A、 周期为的奇函数　　 B、周期为的偶函数　　　

C、周期为的奇函数　　　 D、周期为的偶函数

8．函数的最大值为　　 　　　　（　　）

A．　 　　　 B． 　　　 C．　　　　D．

9. 若（　　　）

A、直角三角形　 B、钝角三角形　C、锐角三角形　D、等腰直角三角形

10、已知f（x）是定义在（0，3）上的函数，f（x）的图象如图所示，那么不等式f（x）cosx＜0的解集是（　　）

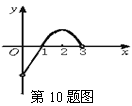A、（0，1）∪（2，3）　B、（1，）∪（，3）

C、（0，1）∪（，3） D、（0，1）∪（1，3）

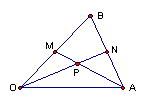11. 在中，，，M为OB的中点，N为AB的中点，P为ON、AM交点，则（　　）

A． B． C． D．

12.稳定房价是我国今年实施宏观调控的重点，国家最近出台的一系列政策已对各地的房地产市场产生了影响，温州市某房地产介绍所对本市一楼群在今年的房价作了统计与预测：发现每个季度的平均单价y（每平方面积的价格，单位为元）与第x季度之间近似满足：，已知第一、二季度平均单价如右表所示：

x	1	2	3
y	10000	9500	？

则此楼群在第三季度的平均单价大约是（　　 ）元

A、 10000　　　B、 9500　　　　C、9000　　　　D、8500

第Ⅱ卷(非选择题　共90分)

二、填空题：本大题共6小题，把答案填在题中横线上.

13、在中, 若, 则的值为_____________;

14、设是两个单位向量，向量，⊥，则=___________;

15、函数的值域是　　　　　　　　  ；

16、已知偶函数的最小正周期是，则f(x)的单调递减区间为　　　　　　　　　　  ；

17、已知点A(－2，4)，B（1，a）,若∠AOB为钝角，则a的取值范围为__________;

18、下列命题：

①若　②若与是共线向量，与是共线向量，则与是共线向量：③若，则④若与是单位向量，则

其中真命题的序号为　　　　　　　　　  。

三、 解答题：

19、已知

（1）求；　（2）求

20、已知向量.

⑴若点A、B、C能构成三角形，求实数m应满足的条件；

⑵若△ABC为直角三角形，且∠A为直角，求实数m的值.

21、已知函数，.求:

(I) 函数的最大值及取得最大值的自变量的集合；

(II) 函数的单调增区间.

22、已知A、B、C三点的坐标分别是A（3，0），B（0，3），C，其中，（1）若，求角的值；

（2）若，求的值.

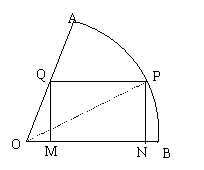
23.如图,在半径为R, 圆心角为60°的扇形AB弧上任取一点P,作扇形的内角矩形PNMQ,使点Q在OA上,点M,N在OB上,求这个矩形面积的最大值及相应的∠AOP的值.

高一数学期中测试题(一)

参考答案

一选择题

题号	1	2	3	4	5	6	7	8	9	10	11	12
选项	A	C	B	A	C	B	D	A	A	C	B	C

二填空题

13. 　　　 14.　　　　 15.[－3, －1] 　　 16. [kπ, kπ+],k∈Z

17.a<且a≠－2　　　 18.③

三、 解答题：

19.【 解析】（1）由

　　　　

　　　　　　　

（2）由

　　　 ∵

　　　∴①当时，矛盾，故舍去.

②当可取.

因此

20. 【 解析】　①已知向量

若点A、B、C能构成三角形，则这三点不共线，

　 

故知　　∴实数时，满足的条件

（若根据点A、B、C能构成三角形，必须AB+BC＞CA…相应给分）

②若△ABC为直角三角形，且∠A为直角，则，

…………10分　解得 .

21.【解析】(I) 解法一:

当,即时, 取得最大值.

函数的取得最大值的自变量的集合为.

解法二:

当,即时, 取得最大值.

函数的取得最大值的自变量的集合为.

(II)解:

由题意得:

即:

因此函数的单调增区间为.

22.【解析】（1）

　　　　

∵

∴=

解得，=1

∵，∴

（2）∵　 ∴

　　　　解得，

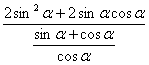　　　　而==2

　　　　=

23.【 解析】 如图,连接OP,则OP=R,设∠POB=α,在Rt△PON中,

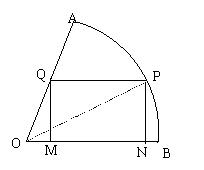PN=Rsinα,ON=Rcosα.

∵四边形PNMQ为矩形, ∴MQ= PN=Rsinα,

∵∠AOB=60°,

∴在Rt△OMQ中,OM=MQcot60°=Rsinα,

∴MN=ON－OM= Rcosα－ Rsinα.

设矩形的面积为S,则

S== Rsinα(Rcosα－Rsinα)

=R²(sinαcosα－sin²α)

=R² (sin2α－)

=R²(sin2α+cos2α) －R²

=R²(sin2α+cos2α)－R²

=R²(sin2αcos30°+cos2αsin30°)－R²

=R²sin(2α+30°)－R²

∵当2α+30°=90°时, sin(2α+30°)_max=1,

∴当α=30°时,S _max=R²－R²=R².

∴矩形面积的最大值是R²,此时∠AOP=30°.