高一数学期中复习二
一.选择题:(每小题5分)
1. 如果
，
，
，那么
等于（ ）
A.
B. 
C. 
D. 
2. 已知函数
为偶函数，且定义域为
则
的值分别为（ ）
A．
B. 
C.1，0
D. 0 ， 1
3. 下列函数中，既是奇函数，又是增函数的是（ ）
A. 
B. 
C. 
D. 
4. 函数y=xx的图象大致是 （ ）
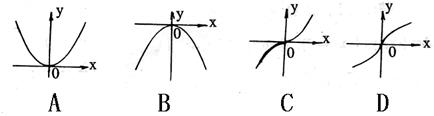
5．已知
，且
，则
的取值范围是（ ）
A. 
B. 
C. 
D. 
6．把函数
的图象向左、向下分别平移2个单位，得到的图象，则
：
A.
B.
C.
D. 
7. 函数
的单调递增区间是（ ）
A. 
B. 
C. 
D. 
8．下列各组函数中，表示同一函数的是
A．
B. 
C.
D. 
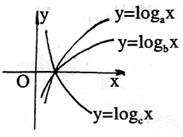
9．由图可推得a、b、c的大小关系是 （ ）
A．c<b<a B．c<a<b
C．a<b<c D．a<c<b
1.
10．奇函数在
上是增函数，又
，则
等于：
A．
B. 
C. 
D. 
11．已知集合A={y y=x2-4x+3,x∈R},B={y y= －x2－2x+2,x∈R}则A∩B等于
A Φ B R C {-1,3} D [-1,3]
12．已知
，则
的大小关系为: （ ）
A
B
C． 
D． 
二.填空题:（每小题4分）
 |
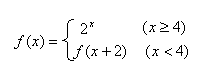13. 已知函数
，那么
.
14．已知函数
的定义域是[－1,1],则
的定义域是__________ 。
15．函数
的定义域为R，则实数的取值范围是
.
16. 函数
在区间
上的最大值为4，则实数
的值为
三. 解答题：
17．（本题满分12分）已知集合A=
若
,求实数a的取值范围.
18.(本题满分12分) 已知函数
（为常数，且
），满足
有唯一解
(1)求函数的解析式 (2)
的值。
19．（本题满分12分）某桶装水经营部每天的房租、人员工资等固定成本为200元，每桶水的进价是5元，销售单价与日均销售量的关系如表所示：
| 销售单价\元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量\同 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
20．已知函数
，
（1）求的定义域；
（2）判断的奇偶性，并予以证明；
（3）判断的单调性，并予以证明.
21．设函数
在区间 [2，4] 上为单调递增函数，
求的取值范围.
22．（本题满分14分）已知
（1）求的定义域；
（2）求的单调区间。
高一数学期中复习二答案
一. AACCD,CBDBD,DD.
二.
13.
,14.[
，4]，15.[0，
，16.-3或
.
三.
17.
或
或
.
18.（1）
,(2)
19.
20(1)(-1,1) (2)奇函数（3）增函数
21.
22.（1）
（x>3）,定义域为
（2）（3，+
）减函数.