高一数学上学期12月第三次月考试题
YCYYCY
说明：1．测试时间：120分钟 总分：150分
2．客观题主观题答在答题纸上
第Ⅰ卷
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知
f ( x ) = 
+ 1 ，则 f ( 0 ) = （ ）
A．－1 B．0 C．1 D．2
2．等差数列{an}的前n项和记为Sn，若
= （ ）
A．24 B．26 C．28 D．30
3．
（ ）
A．4 B．3 C．2 D．1
4．已知函数f(x)的图象过点（0，1），则f(4－x)的反函数的图象过点 （ ）
A．（1，4） B．（4，1） C．（3，0） D．（0，3）
5．若
则 （ ）
A．
B．
C．
D．
6．函数y=loga(2－ax)，其中a>0且a≠1，在[0，1]上是减函数，则实数a的取值范围是（ ）
A．（1，2） B．（0，2） C．（0，1） D．（2，+∞）
7．设函数
是R上的减函数，则有 （ ）
A．
B．
C．
D．
8． 已知函数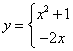
，使函数值为5的
的值是 （ ）
A．-2 B．2或
C． 2或-2 D．2或-2或
9．函数
的定义域是 （ ）
A．
B．
C．
D．
10．函数f(x)=log2x，g(x)=－x2+2，则f(x)·g(x)的图象只可能是 （ ）
|
11．若数列{an}的通项
，则此数列的最大项的值是 （ ）
A．107 B．108 C．108
D．109
12．已知
，那么
等于 （ ）
A．
B．8 C．18 D．
第Ⅱ卷
二、填空题：本大题共4小题，每小题4分共16分。
13．数列1，3，5，7，9，11，……的一个通项公式为an= .
14．函数
的定义域为
。
1５．函数
的值域是
．
16．给出以下命题：
(1)函数
上是减函数；
（2）数列{an}为等差数列的一个充要条件是它的前n项和具有Sn=An2+Bn(A，B为常实数)的形式；
（3）若函数y=ln(ax2+2x+1)的值域为R，则实数a的取值范围是0≤a≤1.
. 其中真命题的序号是 .
三、解答题（本大题共６小题，共７４分）解答应写出文字说明、演算步骤或证明过程。
17．（本题满分12分）求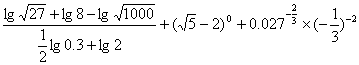
的值。
18．（本题满分12分）等差数列
。
19．已知函数
满足
．(12分)
（1）求的解析式；
（2）当
时，
，求函数
的反函数
.
20．（本小题满分12分）
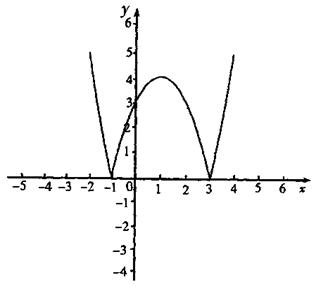
设函数
。
|
的零点；
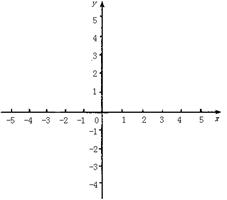
（Ⅱ）在给出的坐标系中直接画出函数的图象，并写出单调区间。
21．（本题满分12分）已知方程
有正实数根，求b的取值范围。
22．（本题满分１２分）函数f(x)对任意的a、b∈R，都有f(a＋b)=f(a)＋f(b)－1，并且当x>0时，f(x)>1．
（1）求证：f(x)是R上的增函数；
（2）若f(4)=5，解不等式f(3m2－m－2)<3．
参 考 答 案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 |
| D | B | B | A | D | A |
| 7 | 8 | 9 | 10 | 11 | 12 |
| D | A | C | C | B | D |
二、填空题
13．2n-1
１４．
1５．（0，1］ 16．②
三、解答题
17．解：∵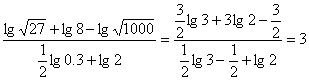
…………8分
原式=3+1+
………………12分
18．解：
………………4分
d=－3
………………6分
…………8分
整理得 n2－13n+36=0
n=4或9 ………………12分
19．
．。。。。。。。。。。。。。。。。。。。。。。6分
（2）
，
19．。。。。。12分
20．（本小题满分12分）
解：（Ⅰ）由
得
即
解得
∴函数的零点为－1，3.……………………………………………4分
|
…………………………… 8分
单调减区间为
单调增区间为
…………………………………………… 12分
21。解：由原方程得
则x2－2（1－logab）x + 1 = 0 。。。。。。。。。。。4分
由原方程有正实数根得，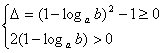
。。。。。。。。。。。8分
得logab≤0 当a＞1时，0＜b≤1；（10分）。。。。。。。。。 10分
当0＜a＜1时，b≥1（12分）。。。。。。。。12分
22、（1）证明：设x1<x2，则△x=x2－x1>0，
∴f(△x)>1，
f(x2)－f(x1)=f(x1＋△x)－f(x1)
=f(x1)＋f(△x)－1－f(x1)=f(△x)－1>0，
∴f(x)是R上的增函数． 。。。。。。。。 7分
（2）解：∵f(4)=f(2＋2)=2f(2)－1=5，∴f(2)=3．
又∵f(x)是R上的增函数，
∴f(3m2－m－2)<3
f(3m2－m－2)<f(2) 。。。。。。。。 12分
3m2－m－2<2－1<m<
，
解得不等式解集为{m－1<m<}．。。。。。。。。。。 １4分