高一数学上学期期末考试模拟题
总分150分
一、选择题:(本大题共10个小题,每小题5分,共50分)
1、已知集合![]() ,
,![]() ,则
,则![]() =( )
=( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D) ![]()
2、在等差数列![]() 中,若它的前n项之和
中,若它的前n项之和![]() 有最大值,且
有最大值,且![]() ,那么当
,那么当![]() 是最小正数时,n的值为( )
是最小正数时,n的值为( )
A、1 B、18 C、19 D、20
3、如果函数![]() 在区间
在区间![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)
![]()
4、函数![]() 的反函数是( )
的反函数是( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D)![]()
5、设![]() 是简单命题,则
是简单命题,则![]() 为真,是
为真,是![]() 为真的( )
为真的( )
(A) 充分不必要条件 (B)必要不充分条件 (C) 充要条件 (D) 既不充分也不必要条件
6、给出函数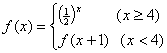 ,则
,则![]() 等于( )
等于( )
(A)![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)
![]()
7、已知![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、已知数列![]() 的通项公式
的通项公式![]() ,其前
,其前![]() 项和
项和![]() 达到最大值时
达到最大值时![]() 的值是( )
的值是( )
(A)26 (B)25 (C)24 (D)23
9、已知等差数列![]() 中,
中,![]() ( )
( )
A、42 B、22 C、21 D、11
10、已知![]() 是三角形的一内角,且
是三角形的一内角,且![]() 则
则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(本大题共5个小题,每小题5分,共25分)
11、数列![]() 的前n项和
的前n项和![]() ,则其通项公式为
.。
,则其通项公式为
.。
12、已知![]() 均为锐角,
均为锐角,![]() ,则
,则![]()
13、设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,已知
项和,已知![]() ,
,![]() ,若
,若![]() ,则
,则![]() =
=
14、定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,则
,则![]()
![]() = 。
= 。
15、 给出下列函数:
①
函数![]() 与函数
与函数![]() 的定义域相同; ②函数
的定义域相同; ②函数![]() 与函数
与函数![]() 值域相同;
值域相同;
③函数![]() 与函数
与函数![]() 在
在![]() 上都是增函数;
上都是增函数;
④函数![]() 的定义域是
的定义域是![]() 。其中错误的序号是
。
。其中错误的序号是
。
三、解答题(本大题共6小题,共75分。解答应写出文字说明,证明过程或演算步骤)
16、(12分)已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
17、(12分)若等比数列![]() 中,已知
中,已知![]() ,数列
,数列![]() 满足
满足![]() 。
。
(1)求证![]() 是等差数列 (2)求
是等差数列 (2)求![]() 的前
的前![]() 项和。
项和。
18、(12分)等比数列![]() 同时满足下列三个条件:①
同时满足下列三个条件:①![]() ;②
;②![]() ;③三个数
;③三个数![]() 依次成等差数列,求数列
依次成等差数列,求数列![]() 的通项公式及前n项和
的通项公式及前n项和![]() 。
。
19、(12分)已知![]() =
=![]()
(1)化简![]() ;(2)若sin=(x+
;(2)若sin=(x+![]() )=
)=![]() ,且
,且![]() <x<
<x<![]() ,求
,求![]() 的值.
的值.
20、(12分)已知函数![]() 的图象过点
的图象过点![]() 和
和![]() ,
,
①
求函数![]() 的解析式;② 函数
的解析式;② 函数![]() 的反函数;③设
的反函数;③设![]() 是正整数,数列的前n项和是
是正整数,数列的前n项和是![]() ,解关于的不等式
,解关于的不等式![]() 。
。
21、已知二次函数![]() R)满足
R)满足![]()
(I)求b的值; (II)当![]()
(III)对于(II)中的![]() 上恒成立,求实数m的取值范围。
上恒成立,求实数m的取值范围。
参考答案
一、1.A ;2.B;3.C;4.A;5.B;6.C;7.D;8.C; 9.D;10.B
二、11. 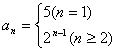 12.
12.![]() 13.1; 14.
13.1; 14.![]() ; 15.①②③.
; 15.①②③.
三、16. ∵![]()
![]() ∴
∴![]() 又∵
又∵![]() ,
,![]()
∴![]() ,
,![]() ∴
∴![]()
∴![]()
![]()
17. (1)因为![]() 是等差数列,
是等差数列,![]() 显然
显然![]()
所以![]() 时,
时,![]()
那么![]() (常数)故
(常数)故![]() 是等差数列
是等差数列
(2)由(1)知![]() 是等差数列,
是等差数列,![]() 所以
所以![]()
18.(1) ![]() ;
;![]()
19.(1)![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]()
20解(Ⅰ)f(x)=![]() =
=![]()
=![]() =2
=2![]() 或(1-cos2x)
或(1-cos2x)
(Ⅱ)∵sin(x+![]() )=
)=![]() 且
且![]() <x<
<x<![]()
∴![]() <x+
<x+![]() <
<![]() ∴cos(x+
∴cos(x+![]() )=-
)=-![]() ∴sin2(x+
∴sin2(x+![]() )=2sin(x+
)=2sin(x+![]() )cos(x+
)cos(x+![]() )
)
=2·![]() ·(-
·(-![]() )=-
)=-![]() 即:sin(2x+
即:sin(2x+![]() )=-
)=-![]() 得cos2x=-
得cos2x=-![]() ∴f(x)=1-cos2x=1-(-
∴f(x)=1-cos2x=1-(-![]() )=
)=![]()
21. 解:(I)![]() 解得
解得![]() .(或利用对称性求解)
.(或利用对称性求解)
(II)由(I),![]()
![]()
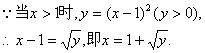
![]() .
.
(III)![]()
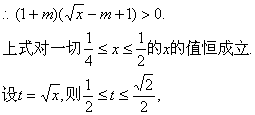
![]() ……3分
……3分
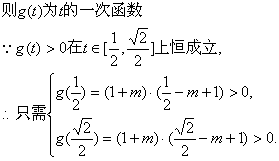
解得![]()
![]() 的取值范围是
的取值范围是![]() .
.