高一数学上学期期末综合练习
测试内容:集合、函数、数列(时间:120分钟) 总分120分
一.选择题(每小题5分,共60分)
1.下列图像中,不可能是函数图像的是
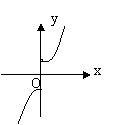
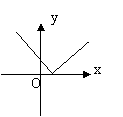
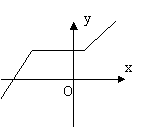
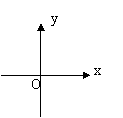

(A) (B) (C) (D)
2.函数![]() 在
在![]()
![]() 上最小值为
上最小值为
A.0 B.![]() C.
C.![]() D.以上都不对
D.以上都不对
3.函数![]()
![]() 的值域是
的值域是
![]()
![]()
![]()
![]()
4.下列函数中,值域为![]() 是
是
![]()
![]()
![]()
![]()
5.下列四组函数f(x)、g(x),表示同一函数的是
A、f(x)=1, g(x)=x0 B、f(x)=x+1, g(x)=![]()
C、f(x)=x2,
g(x)=![]() D、f(x)=x3, g(x)=
D、f(x)=x3, g(x)=![]()
6.函数y=2-x+1(x>0),的反函数是
A、![]() x∈(1,2) B、
x∈(1,2) B、![]() x∈(1,2)
x∈(1,2)
C、![]() x∈(1,2) D、
x∈(1,2) D、![]() x∈(1,2)
x∈(1,2)
7. 某商品零售价2006年比2005年上涨25%,欲控制2007年比2005年只上涨10%,则2007年应比2006年降价( )
A、15% B、12% C、10% D、50%
8.设![]() 与
与![]() 都是函数
都是函数![]() 的单调区间,
的单调区间,![]() 且
且![]() ,则
,则![]() 与
与![]() 的大小关系为
的大小关系为
![]()
![]()
![]()
![]() 不能确定
不能确定
9.定义在R上的函数![]() ,设
,设![]() ,给出下列不等式:
,给出下列不等式:
①![]() ; ②
; ②![]() ;
;
③![]() ;
;
④![]() 其中正确序号是
其中正确序号是
A.①③ B.①④ C.②③ D.②④
10.定义在R上的函数![]() 对于任意两个不等实数
对于任意两个不等实数![]() 总有
总有![]() 成立,
成立,
则必有
A. 函数![]() 是奇函数
B. 函数
是奇函数
B. 函数![]() 是偶函数
是偶函数
C. 函数![]() 在R上是增函数 D. 函数
在R上是增函数 D. 函数![]() 在R上是减函数
在R上是减函数
11.已知函数![]() 在区间
在区间![]() 上具有单调性,且
上具有单调性,且![]() 则方程
则方程![]() 在区间
在区间![]() 上
上
A.至少有一个实根 B.至多有一个实根 C.无实根 D.必有唯一实根
12.函数y=lgx和y=![]() 的图象关于(*)
的图象关于(*)
A.x轴对称 B.y轴对称
C.y=x对称 D.原点对称
二.填空题(每小题4分,共16分)![]()
13.![]() 在区间
为增函数,在区间
上为减函数。
在区间
为增函数,在区间
上为减函数。
14.不等式![]() 在R内恒成立,则
在R内恒成立,则![]() 的取值范围是
。
的取值范围是
。
15.函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() 的取值范围是
。
的取值范围是
。
16.乙知![]() ,则
,则![]() 。
。
三.解答题:(4大题,共44分)
17.(本小题12分)已知:函数![]() 在区间
在区间![]() 上的最大值是4,求
上的最大值是4,求![]() 的值。
的值。
18. (本小题12分)某商品在近30天内每件的销售价格![]() 元与时间
元与时间![]() 天的函数关系式是
天的函数关系式是
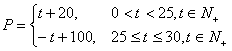
该商品的日销售量![]() (件)与时间
(件)与时间![]() (天)的函数关系式是
(天)的函数关系式是![]() (
(![]() ),求这种商品的日销售金额的最大值,并指出取得该最大值的一天是30天中的第几天?
),求这种商品的日销售金额的最大值,并指出取得该最大值的一天是30天中的第几天?
19. (本小题10分)已知二次函数![]() ,当
,当![]() 时,试证:
时,试证:
(1)
当![]() 时,
时,![]() 是递减函数;
是递减函数;
(2)
当![]() 时,
时,![]() 在定义域内至少有一个
在定义域内至少有一个![]() ,使
,使![]() 成立。(反证法)
成立。(反证法)
20.( 本小题10分)设有函数![]() ,当
,当![]() 时,
时,![]()
(1)若![]() 为
为![]() 上的奇函数,能否确定
上的奇函数,能否确定![]() 的解析式?
的解析式?
(2)若![]() 为
为![]() 上的偶函数,能否确定
上的偶函数,能否确定![]() 的解析式?
的解析式?
答案:
1—12: DBDDD AABBC DA
13.增区间为![]() ,减区间为
,减区间为![]() ;
;
14.![]() ;
;
15.![]()
16.1
17.解:![]() ,区间
,区间![]() 上的中点是
上的中点是![]() ,函数的对称轴为
,函数的对称轴为![]() ,结合二次函数的图像,
,结合二次函数的图像,
当![]() 即
即![]() 时,
时,![]() ,所以
,所以![]() ,且
,且![]() 。
。
当![]() 即
即![]() 时,
时,![]() ,所以
,所以![]() ,且
,且![]() 。
。
综上所述,![]() 。
。
18.解:射日销售额为![]() 元。
元。
则![]() ,
,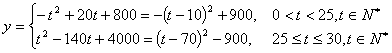
当![]() 时,
时,![]() ,
,![]() (元);
(元);
当![]() 时,
时,![]() (元)。
(元)。
![]() 所以
所以![]() (元),故所秋日销售金额的最大值为1125元,且在最近30天中的第25天日销售金额最大。
(元),故所秋日销售金额的最大值为1125元,且在最近30天中的第25天日销售金额最大。
19.解;(1)![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() ,
,
当![]() 时,
时,![]() 。由图象可知:当
。由图象可知:当![]() 时,
时,![]() 为递减函数。
为递减函数。
(2)设在![]() 内,
内,![]() 不成立,则
不成立,则![]() 。
。
由于![]() ,
,
联立可推出![]() ,与
,与![]() 相矛盾。
相矛盾。
所以,假设不成立 ,故原命题成立。
20.(1)因为![]() 位R上的奇函数,故当
位R上的奇函数,故当![]() 时,
时,
有:![]() 。
。
又![]() ,所以
,所以![]() 的解析式可如下确定
的解析式可如下确定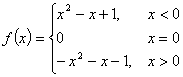
(2)因为![]() 位R上的偶函数,故当
位R上的偶函数,故当![]() 时,
时,
有:![]()
但![]() 无法确定,所以
无法确定,所以![]() 的解析式可如下确定
的解析式可如下确定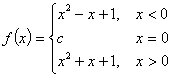 ,
,
其中c为任意常数,故![]() 不能为以确定。
不能为以确定。