新课标高一数学同步测试（5）—第一单元测试题
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）。
1．用描述法表示一元二次方程的全体，应是 （ ）
A．｛x｜ax2+bx+c=0，a，b，c∈R｝
B．｛x｜ax2+bx+c=0，a，b，c∈R，且a≠0｝
C．｛ax2+bx+c=0｜a，b，c∈R｝
D．｛ax2+bx+c=0｜a，b，c∈R，且a≠0｝
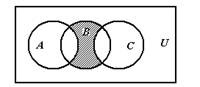
2．图中阴影部分所表示的集合是（ ）
A.B∩［CU(A∪C)］ B.(A∪B) ∪(B∪C)
C.(A∪C)∩(CUB) D.［CU(A∩C)］∪B
3．设集合P=｛立方后等于自身的数｝，那么集合P的真子集个数是 （ ）
A．3 B．4 C．7 D．8
4．设P=｛质数｝，Q=｛偶数｝，则P∩Q等于 （ ）
A． B．2 C．｛2｝ D．N
5．设函数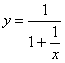
的定义域为M，值域为N，那么 （ ）
A．M=｛x｜x≠0｝，N=｛y｜y≠0｝
B．M=｛x｜x＜0且x≠－1，或x＞0
，N=
y｜y＜0，或0＜y＜1，或y＞1
C．M=｛x｜x≠0｝，N=｛y｜y∈R｝
D．M=｛x｜x＜－1，或－1＜x＜0，或x＞0＝，N=｛y｜y≠0｝
6．已知A、B两地相距150千米，某人开汽车以60千米/小时的速度从A地到达B地，在B地停留1小时后再以50千米/小时的速度返回A地，把汽车离开A地的距离x表示为时间t（小时）的函数表达式是 （ ）
A．x=60t B．x=60t+50t
C．x=
D．x=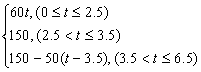
7．已知g(x)=1-2x,f[g(x)]=
,则f(
)等于 （ ）
A．1 B．3 C．15 D．30
8．函数y=
是（ ）
A．奇函数 B．偶函数 C．既是奇函数又是偶函数 D．非奇非偶数
9．下列四个命题
（1）f(x)=
有意义;
（2）函数是其定义域到值域的映射;
（3）函数y=2x(x
)的图象是一直线；
（4）函数y=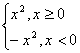
的图象是抛物线，其中正确的命题个数是 （ ）
A．1 B．2 C．3 D．4
10．设函数f (x)是（－
，+）上的减函数，又若a
R，则 （ ）
A．f (a)>f (2a) B ．f (a2)<f (a)
C ．f (a2+a)<f (a) D．f (a2+1)<f (a)
二、填空题：请把答案填在题中横线上（每小题6分，共24分）.
11．设集合A={
},B={x
},且A
B，则实数k的取值范围是
.
12．函数f(x)的定义域为[a,b],且b>-a>0,则F（x）= f(x)-f(-x)的定义域是 .
13．若函数 f(x)=(K-2)x2+(K-1)x+3是偶函数，则f(x)的递减区间是 .
14．已知x[0,1],则函数y=
的值域是
.
三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分).
15．（12分）已知，全集U={x-5≤x≤3}，
A={x-5≤x<-1}，B={x-1≤x<1},求CUA，
CUB，(CUA)∩(CUB)，(CUA)∪(CUB)，
CU(A∩B)，CU(A∪B)，并指出其中相关的集合.
16．（12分）集合A={（x,y）
},集合B={（x,y）
,且0
}，又A
，求实数m的取值范围.
17．（12分）已知f(x)=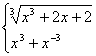
,求f[f(0)]的值.
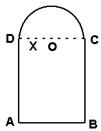
18．（12分）如图，用长为1的铁丝弯成下部为矩形，上部为半圆形的框
架，若半圆半径为x，求此框架围成的面积y与x的函数式y=f (x)，
并写出它的定义域.
19．（14分）已知f (x)是R上的偶函数，且在(0,+ )上单调递增，并且f (x)<0对一切
成立，试判断
在(－,0)上的单调性，并证明你的结论.
20．（14分）指出函数
在
上的单调性，并证明之.
参考答案（5）
一、DACCB DCBA D
二、11．{
}； 12．[a,-a]； 13．[0，+]； 14．[
] ；
三、15． 解： CUA={x-1≤x≤3}；CUB={x-5≤x<-1或1≤x≤3}；
(CUA)∩(CUB)= {x1≤x≤3}；(CUA)∪(CUB)= {x-5≤x≤3}=U；
CU(A∩B)=U；CU(A∪B)= {x1≤x≤3}.
相等集合有(CUA)∩(CUB)= CU(A∪B)；(CUA)∪(CUB)= CU(A∩B).
16． 解：由A
B
知方程组
得x2+(m-1)x=0 在0
x
内有解， 
即m
3或m-1.
若m3，则x1+x2=1-m<0,x1x2=1,所以方程只有负根.
若m-1,x1+x2=1-m>0,x1x2=1,所以方程有两正根，且两根均为1或两根一个大于1，一个小于1，即
至少有一根在[0，2]内.
因此{m
<m-1}.
17．解： ∵ 0（-
）， ∴f(0)=
,又
>1，
∴
f()=()3+()-3=2+=
,即f[f(0)]=.
18．解：AB=2x, 
=
x,于是AD=
， 因此，y=2x· 
+
，
即y=-
.
由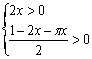
，得0<x<
函数的定义域为（0，
）.
19．解：设x1<x2<0, 则 － x1 > － x2 >0, ∴f(－x1)>f(－x2), ∵f (x)为偶函数, ∴f(x1)>f(x2)
又
（∵f(x1)<0,f(x2)<0）∴
∴
是(,0)上的单调递减函数.
20．解：任取x1，x2
且x1<x2 
由x1<x2—1知x1x2>1, ∴
, 即
∴f(x)在上是增函数；当1x1< x2<0时，有0< x1x2<1,得
∴
∴f(x)在
上是减函数.
再利用奇偶性，给出
单调性，证明略.