高一数学同步讲练同步—三角函数的最值
一、知识回顾
1、求三角函数最值的常用方法有：（1）配方法；（2）化为一个角的三角函数形式，如
等，利用三角函数的有界性求解；（3）数形结合法；（4）换元法；（5）基本不等式法等.
2、三角函数的最值都是在给定区间上取得的，因而特别要注意题设中所给出的角的范围，还要注意弦函数的有界性.
二、基本训练
1、设函数
，则
的最大值是
.
2、函数
的最小值是
.
3、函数
在区间
上的最小值是 （ ）
A、
B、
C、－1 D、
4、函数
的最大值是 ，最小值是 .
5、函数
在
上的最小值是
.
三、例题分析
例1、求函数
的最值，并求取得最值时的
值.
例2、求
的最大值和最小值.
例3、求函数
的最值.
例4、已知
，求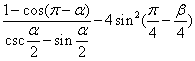
的最大值及取得最大值的条件.
例5、（05江西卷）
已知向量
.
求函数f(x)的最大值，最小正周期，并写出f(x)在[0，π]上的单调区间.
例6、（05重庆卷）若函数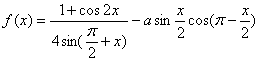
的最大值为2，试确定常数a的值.
四、作业 同步练习g3.1050三角函数的最值
1、函数
的值域为 （ ）
A、
B、[－1,3] C、[0,
3] D、[－3, 0]
2、若
，则
的最大值和最小值分别是 （ ）
A、7, 5 B、7，
C、5， D、7，－5
3、当函数
取得最大值时，
的值是 （ ）
A、
B、
C、
D、4
4、（05全国卷Ⅰ）当
时，函数
的最小值为
（A）2 （B）
（C）4 （D）
5、.(05浙江卷)已知k＜－4，则函数y＝cos2x＋k(cosx－1)的最小值是( )
(A) 1 (B) －1 (C) 2k＋1 (D) －2k＋1
6、（05上海卷）函数
的图象与直线
有且仅有两个不同的交点，则
的取值范围是__________。
7、
的最大值是＿＿＿＿＿。
8、函数
的最小值是＿＿＿＿＿＿。
9、求
的最值。
10、求函数
的最大值和最小值。
11、设关于的函数
的最小值为
（1）试用
写出
的表达式；
（2）试确定
的值，并对此时的求出
的最大值。
12、求函数
的最大、最小值。
答案：
基本训练、1、
2、
3、D 4、
；－1 5、3
例题分析、例1、当
时，
，当
时，
例2、
，
例3、
，
例4、当
时，最大值为0
例5、解：
=
.
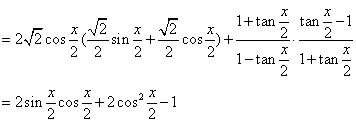
所以
，最小正周期为
上单调递增，
上单调递减.
例6、
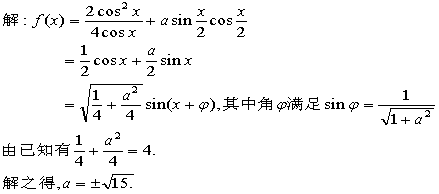
作业、1—5、BDBCA
6、
7、
8、
9、
10、0 
11、（1）
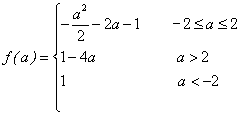（2）
12、