高一数学训练题
一、选择题：（每小题5分，共50分）
1．若集合
，则满足
的集合B的个数（ ）
A．1 B．2 C．7 D． 8
2．
的一个必要不充分条件是( )
A、
B、
C、
D、
3．若函数
的定义域为
，则函数
的定义域为（ ）
A．
B．
C．
D．
| |
，其中[x]表示不超过x的最大整数，如[3.1]=3,则f(-3.5)=
A.-2
B.
C.1
D.2
5. 
的分数指数幂表示为
A．
B. a 3 C.
D、都不对
6．设
，则
的大小关系是
A．
B．
C．
D．
7．方程
的实数解是个数为（ ）
A． 1个 B． 2个 C． 3个 D． 0个
8．已知
，则函数
（ ）
A．有最小值
，但无最大值
B．有最小值，有最大值1
C．有最小值1，有最大值
D．无最小值，也无最大值
9．函数y=log
(2x2-3x+1)的递减区间为（ ）
A．（1，+
）
B。（-，
］
C．（
，+）
D。（-，］
10．将函数的图象沿X轴（ ）所得图象与的图象关于Y轴对称。
A．向右平移一个单位 B。向左平移一个单位
C．向上平移一个单位 D。向下平移一个单位
二、填空题：（每小题5分，共25分）
11．函数
的定义域为__________________．
12．函数y=log(x2-6x+17)的值域是___________________.
13．
的值是__________________．
14．设函数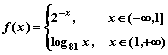
，若
，则
__________．
15．若
，求实数
的取值范围______________.
一、选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题答题卡
11．_________________ 12．________________
13．________________ 14．________________
15．________________
三、解答题：
16.(本小题12分)已知A={xx-a＜4}，B={xx2-x-6＞0}且A∪B=R，求a的取值范围。
17、（本小题满分12分）函数f（x）对任意的m∈R都有f（m+2）=f（m）+2且f（x）为增函数，若
f（3）=4
（1）求f（1）。
（2）若f（a2+a-5）＜2，求a的取值范围。
18.（本小题12分）若关于x的方程
+2x·a+a+1 =0有实数根，求实数a的取值范围。
19.(本小题12分)已知函数f(x)=
。
（1）判断f(x)的单调性；
（2）求f-1(x)。
20.（本小题13分）某小型自来水厂的蓄水池中存有400吨水，自来水厂每小时可向蓄水池中注入水60吨，同时蓄水池又想居民区不间断地供水，
小时内供水总量为
吨。若蓄水池中水量少于80吨，就会出现供水紧张现象。试问在一天的24小时内，有几小时出现供水紧张现象？并说明理由。
21．（本小题14分）已知x满足不等式2(log2x）2-7log2x+3
0,求函数f(x)=log2
的最大值和最小值。
参考答案
一、选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | A | C | C | B | B | C | A | A |
二、填空题答题卡
11．
12．
13．3 14．3
15．
三、解答题：
16.(本小题12分)已知A={xx-a＜4}，B={xx2-x-6＞0}且A∪B=R，求a的取值范围。
解：A={x x-a＜4}
={xa-4＜x＜a+4}
B={xx2-x-6＞0}
={xx＞3或x＜-2}（6分）
A∪B=R 则 a-4＜-2
a+4＞3
∴-1＜a＜2
则a的取值范围是-1＜a＜2
17、（本小题满分12分）函数f（x）对任意的m∈R都有f（m+2）=f（m）+2且f（x）为增函数，若f（3）=4
（1）求f（1）。
（2）若f（a2+a-5）＜2，求a的取值范围。
解：（1）令m=1 则f（3）=f（1）+2
又f（3）=4 则f（1）+2=4
∴f（1）=2（6分）
（2）f（a2+a-5）＜2 
f（a2+a-5）＜f（1）
又f（x）是增函数，则a2+a-5＜1
∴a2+a-6＜0
即-3＜a＜-2
则a的取值范围是-3＜a＜2
18.（本小题12分）若关于x的方程+2x·a+a+1 =0有实数根，求实数a的取值范围。
解：（2x）2+a(2x)+a+1=0有实根，∵ 2x>0,∴相当于t2+at+a+1=0有正根，
则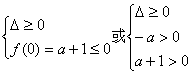
解得
提示：也可以用变量分离法。
19.(本小题12分)已知函数f(x)=。
（1）判断f(x)的单调性；
（2）求f-1(x)。
解：1）f(x)=
，
,且x1<x2,f(x1)-f(x2)=
<0,(∵102x1
<102x2)∴f(x)为增函数。
（2）由y=
得102x=
∵102x>0,
∴-1<y<1,又x=
)。
20.（本小题13分）某小型自来水厂的蓄水池中存有400吨水，自来水厂每小时可向蓄水池中注入水60吨，同时蓄水池又想居民区不间断地供水，小时内供水总量为吨。若蓄水池中水量少于80吨，就会出现供水紧张现象。试问在一天的24小时内，有几小时出现供水紧张现象？并说明理由。
解：由题意，小时后蓄水池中水量为
＜80令
，则有
4＜x＜8，即
.
故在一天内有8小时会供水紧张.
21．（本小题14分）已知x满足不等式2(log2x）2-7log2x+30,求函数f(x)=log2的最大值和最小值。
解：由2（log2x）2-7log2x+30解得log2x3。∵f(x)=log2
(log2x-2)=(log2x-
)2-
,∴当log2x=时，f(x)取得最小值-；当log2x=3时，f(x)取得最大值2。