高一数学第一学期期中考试试卷
试卷满分：150分 考试时间：120分钟
第Ⅰ卷（选择题，共60分）
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个是符合题目要求的。）
1．已知集合
，那么
的真子集的个数是（ ）
A、15 B、16 C、3 D、4
2．若
，则
（ ）
A、10
B、4
C、
D、2
3. 不等式（x＋1）（2－x）＞0的解集为 （ ）
A、
B、
C、
D、
4．下列各组函数中，表示同一函数的是 （ ）
A 、
B、
C 、
D、
5．函数
的定义域为[4，7]，则
的定义域为
A、（1，4） B [1，2]
C、
D、 
6．若
能构成映射，下列说法正确的有
（ ）
（1）A中的任一元素在B中必须有像且唯一；（2）B中的多个元素可以在A中有相同的原像；（3）B中的元素可以在A中无原像；（4）像的集合就是集合B。
A、1个 B、2个 C、3个 D、4个
7．若函数
在区间
上是减函数，则实数
的取值范围是
A、
B、
C、
D、
8．定义域为R的函数y=f(x)的值域为[a，b]，则函数y=f(x＋a)的值域为 （ ）
A．[2a，a＋b] B．[a，b] C．[0，b－a] D．[－a，a＋b]
9．下列所给4个图象中，与所给3件事吻合最好的顺序为 （ ）
（1）我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学；
（2）我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；
（3）我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速。
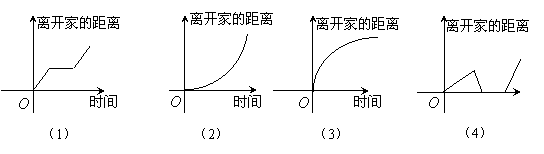A、（1）（2）（4） B、（4）（2）（3） C、（4）（1）（3） D、（4）（1）（2）
10．已知
的图象恒过（1，1）点，则
的图象恒过
A．（－3，1） B．（5，1） C．（1，－3） D．（1，5）
11. 方程x2-6x
=a有不同的四个解，则a的范围是
A、a
9
B、0a9
C、0<a<9 D、0<a9
12、已知集合A={a，b，c}，B={1，2，3，4，5，6}。f：A
是从A到B的映射，则满足f(a)>f(b)=f(c)的映射个数为
A、10 B、15 C、20 D、21
高一数学第一学期期中考试试卷
试卷满分：150分 考试时间：120分钟
一．选择题（本题共12小题，每小题5分，计60分，在每小题给出的四个选项中，只有一个是符合要求的。）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（本题共4小题，每小题4分，共16分）
13．三数
从小到大排列为______________．
14．已知
在定义域
上是减函数，且
，则的取值范围是
15．设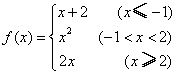
，若
，则
16．如图，把截面半径为25cm的圆形木头锯成矩形木料.如果矩形的一边长为
cm，面积为
cm2.把表示为的函数,
这个函数的解析式为
（须注明函数的定义域）.
三、解答题（本大题共6小题，共74分.解答应写出必要的文字说明，证明过程或演算步骤）
17、(本题满分12分)
解关于x的不等式: 
18、.（本小题满分12分）
已知M={x -2≤x≤5}, N={x a+1≤x≤2a-1}.
（Ⅰ）若M
N，求实数a的取值范围；（Ⅱ）若M
N，求实数a的取值范围.
19、（本题满分12分）已知一次函数f(x)=
,若f(x)是减函数，且f(1)=0,
（1）求m的值； (2)若f(x+1) ≥ x2
, 求x的取值范围。
20、已知函数
的图象经过点
，其中
且
．
(1)求的值； (2) 求函数
的值域.
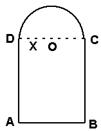21、（本小题满分12分）如图，用长为L的铁丝弯成下部为矩形，上部为半圆形的框架，若半圆半径为x，求此框架围成的面积y与x的函数式y=f (x)，并写出它的定义域.
22、（满分14分）已知函数
是奇函数，且
.
（1）求函数f(x)的解析式；
（2）判断函数f(x)在
上的单调性，并加以证明.
高一数学试卷答案及评分标准
一、选择题
1— 6：A、D、D、C、D、B 7—12：A、B、D、B、C、B
二、填空题：
，14、0<a<2/3, 15、
，
16、
三、解答题
17、解：不等式化为，（x+2）(x-a)≤0
a>-2时，－2≤x≤a
a=-2时， x≠-2
a<-2时，a≤x≤-2
所以，不等式的解集为：a>-2时，｛x︱-2≤x≤a｝;
a=-2时，｛x︱x≠-2｝;a<-2时，｛x︱a≤x≤-2｝;
18、解：（Ⅰ）由于MN，则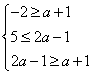
，解得a∈Φ
（Ⅱ）①当N=Φ时，即a＋1＞2a－1，有a＜2
②当N≠Φ，则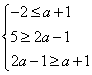
，解得2≤a≤3，.
综合①②得a的取值范围为a≤3
19
20、解：（1）函数图象过点，所以，
，则
．
(2) 
由
得，
于是
所以，所求的函数值域为
．
21、解：由已知，得
AB=2x, 
=
x,
于是AD=
，
因此，y=2x·
+
，
即y=
.
由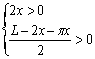
，得0<x<
函数的定义域为（0，
）.
22、解：（1）∵f(x)是奇函数，∴对定义域内的任意的x，都有
，
即
，整理得：
∴q=0
又∵，∴
，
解得p=2 ∴所求解析式为
（2）由（1）可得=
， 设
，
则由于
=
因此，当
时，
，
从而得到
即，
∴
是f(x)的递增区间。