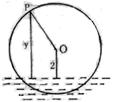
高一数学第一章精选练习
1. 角
的终边上有一点
，则
=（ ）
A.
B.
C.
D.
2. 函数
的周期、振幅依次是( )
A.π、3 B.4π、－3 C.4π、3 D.π、－3
3. 已知扇形的周长是6cm，面积是2cm2,则扇形的中心角的弧度数是（ ）
A.1 B.1或4； C.4 D.2或4
|
则有( )
A．
B．
C．
D．
.
5．设
，那么下列各点在角
终边上的是
（ ）
A．
B．
C．
D．
6．已知
，且
，则
的值为
（ ）
A．
B．
C．
D．
7．若
，则
的值为
（ ）
A．
B．
C．
D．
8．已知函数
，则
（ ）
A．
与
都是奇函数
B．与都是偶函数
C．是奇函数，是偶函数 D．是偶函数，是奇函数
9．函数
的单调递减区间是
（ ）
A．
B．
C．
D．
10．函数
的部分图象是
（ ）
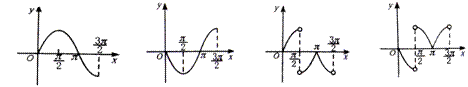
A． B． C． D．
11. 若函数y=2sin(8x+θ)+1的图象关于直线
对称，则θ的值为
A．0 B.
C．kπ(k∈Z) D．kπ+
（k∈Z）
12.实数
满足
，则
的值为 （ ）
(A)
(B)3 (C)4 (D)与
有关
13. 若
是方程
的解,其中
,则
=
14．
的值为
．
15．已知函数
的最小正周期为3
，则A=
．
16. 关于函数f(x)＝4sin(2x＋
) (x∈R)，有下列命题:
①由f(x1)＝f(x2)＝0可得x1－x 2必是π的整数倍；
②y＝f(x)的表达式可以改写成y＝4cos(2x－
)；
③y＝f(x)的图像关于点(－
，0)对称；
④y＝f(x)的图像关于直线x＝－
对称.
其中正确的命题序号是_______.(注:把你认为正确的命题序号都填上)
17. (本题满分12分)设函数
,给出三个论断:1它的图象关于
对称;2它的最小正周期为
;3它在区间
上的最大值为
.以其中的两个论断作为条件,另一个作为结论,试写出你认为正确的一个命题并给予证明.
18．已知函数
是
上
的偶函数，其图象关于点
对称，且在区间
上是单调
函数.求
的值.
（2004辽宁－1）若
，且
，则角
的终边所在象限是
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
（2004内蒙古、海南、西藏、陕西、广西理、文－2）函数
的最小正周期是
（A）
（B）
（C）
（D）
（2004四川、吉林、黑龙江、云南理、文－5）已知函数
的图象过点
，则
可以是
（A）
（B）
（C）
（D）
（2004辽宁－7）已知函数
，则下列命题正确的是
（A）是周期为1的奇函数 （B）是周期为2的偶函数
（C）是周期为1的非奇非偶函数 （D）是周期为2的非奇非偶函数
（2004河南、河北、山东、山西、安徽、江西理、文－9）为了得到函数
的图象，可以将函数
的图象
（A）向右平移个单位长度 （B）向右平移
个单位长度
（C）向左平移个单位长度 （D）向左平移个单位长度
（2004天津理－9，文－10）函数
为增函数的区间是
（A）
（B）
（C）
（D）
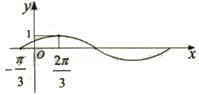（2004辽宁－11）若函数
的图象（部分）如图所示，则
的取值是
（A）
（B）
（C）
（D）
（湖北理、文－12）设
是某港口水的深度
（米）关于时间t（时）的函数，其中
．下表是该港口某一天从0时至24时记录的时间t与水深y的关系：
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察，函数的图象可以近似地看成函数
的图象.下面的函数中，最能近似表示表中数据间对应关系的函数是 （ ）
（A）
（B）
（C）
（D）