高一数学考试试卷（1）
第Ⅰ卷(共50分)
一、选择题（每小题5分，共50分。下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）
1．集合M={1,2,3}的非空真子集的个数是 （ ）
A．6 B.4 C.8 D.7
2．若非空集合A={x2a+1≤x≤3a-5},
B={x3≤x≤22}，则使
成立的所有a的值的集合是
（ ）
A．
B．
C．
D．
3．条件 p： x = x，条件q：x 2 ≥－x，则p是q的 ( )
A．充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 即不充分又不必要条件
4．给出以下判断：
（1）若命题p是真命题，则命题“p且q”一定是真命题.
（2）若命题“p且q”为真命题，则命题p一定是真命题.
（3）若命题p是真命题，则命题“p或q”一定是真命题
（4）若命题“p或q” 为真命题，则命题p一定是真命题。
（5）命题p与“非p”一定是一真一假.
其中正确命题的个数是 （ ）
A．2 B.3 C.4 D.5
5函数
的定义域为
( )
A.[-2,2] B.[-2,1）∪﹙1,2]
C.(-∞,2] D.(-2,1)∪(1,2)
6．函数
（x＞1）的值域是
（
）
A.(-∞，0)∪（0，+∞） B.R
C.（1，+∞） D.（0，1）
7.设
,则
等于
( )
A.
B.
C. 
D.
8.已知函数
对任意t
R都有
，则有（ ）
A.
B.
C. 
D.
9.若函数
在区间
内递减，那么实数
的取值范围是
（ ）
A.
B. 
C.
D.
10.函数
的单调增区间是
( )
A. 
B.
C.
D. 
第Ⅱ卷(共100分)
二、填空题（每题5分，共25分.将正确答案填在答题卡上）
11．设方程
的两根为
，且
，
，则实数
的取值范围是
12．已知
，
，
，则
．
13．已知
，则
=
14．若
与
是定义在区间
上的一对互为反函数，且
在上单调递增，则
和
的大小关系是
15．已知定义域在R上，图像关于y轴对称，那么
三 、解答题(共75分,要求每题都要写出必要的证明或计算过程)
16．（本题满分12分） 求下列函数的反函数
（1）
（2）
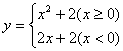
17．（本题满分12分）已知集合
，
，
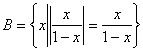且
，
，求a,b的值
18．（本题满分12分）若
恒成立，求函数
的最值。
19．（本题满分12分）已知函数
在区间[0，1]上的最大值是2，求实数的值。
20．（本题满分13分）探究函数
的最小值，并确定取得最小值时x的值.列表如下：
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成以下的问题.
函数
在区间（0，2）上递减；
函数在区间
上递增.
当
时，
.
证明：函数
在区间（0，2）递减.
思考：函数
时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
21．（本题满分14分）设函数
是定义在(0,+∞)上的函数，并且满足下面三个条件：
①对任意正数
，都有
；②当
时，
；③
；
（I）求
、
的值；
（II）证明函数f(x)在(0,+∞)上为减函数。
（III）如果存在正数k，使不等式
有解，求正数
的取值范围．