新课标高一数学期中测试
一、选择题:
1.满足条件![]() 的所有集合A的个数是( )
的所有集合A的个数是( )
A.![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D.![]() 个
个
2.下列四个命题中,设![]() 为全集,则不正确的命题是( )
为全集,则不正确的命题是( )
A.若![]() ,则
,则![]() ;
;
B.若![]() ,则
,则![]() ;
;
C.若![]() ,则
,则![]() ;
;
D.若![]() ,则
,则![]() 。
。
3.函数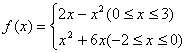 的值域是( )
的值域是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程. 在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
![]() 5.函数
5.函数![]() 的反函数是( )
的反函数是( )
A.![]() (
(![]() ) B.
) B.![]() (
(![]() )
)
C.![]() (
(![]() ) D.
) D.![]() (
(![]() )
)
6.已知![]() 、
、![]() 两地相距
两地相距![]() 千米,某人开汽车以
千米,某人开汽车以![]() 千米/小时的速度从
千米/小时的速度从![]() 地到达
地到达![]() 地,在
地,在![]() 地停留
地停留![]() 小时后再以
小时后再以![]() 千米/小时的速度返回
千米/小时的速度返回![]() 地,把汽车离开
地,把汽车离开![]() 地的距离
地的距离![]() 表示为时间
表示为时间![]() (小时)的函数表达式是( )
(小时)的函数表达式是( )
A.![]() B.
B.![]()
C.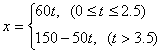 D.
D.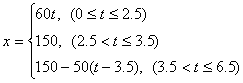
7.函数![]() ,在
,在![]() 上有
上有![]() ,那么( )
,那么( )
A.![]() 在
在![]() 上是增函数 B.
上是增函数 B.![]() 在
在![]() 上是减函数
上是减函数
C.![]() 在
在![]() 上是增函数 D.
上是增函数 D.![]() 在
在![]() 上是减函数
上是减函数
8.某厂去年![]() 月份的产值是
月份的产值是![]() 月份产值的
月份产值的![]() 倍,则该厂去年产值的月平均增长率为( )
倍,则该厂去年产值的月平均增长率为( )
A.![]() B.
B.
![]() C.
C.![]() D.
D.
![]()
9.设![]() 是偶函数,
是偶函数,![]() 是奇函数,那么
是奇函数,那么![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
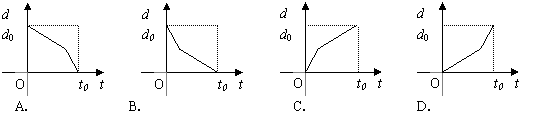
10.某地的中国移动“神州行”卡与中国联通![]() 网的收费标准如下表:
网的收费标准如下表:
| 网络 | 月租费 | 本地话费 | 长途话费 |
| 甲:联通 | | 每分钟 | 每 |
| 乙:移动“神州行”卡 | 无 | 每分钟 | 每 |
(注:本地话费以分钟为单位计费,长途话费以![]() 秒钟为单位计费)
秒钟为单位计费)
若某人每月拨打本地电话时间是长途电话时间的![]() 倍,且每月通话时间(分钟)的范围在区间
倍,且每月通话时间(分钟)的范围在区间![]() 内,则选择较为省钱的网络为( )
内,则选择较为省钱的网络为( )
A. 甲 B. 乙 C. 甲乙均一样 D. 分情况确定
二、填空题
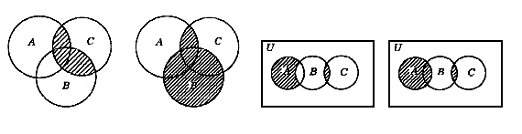
11.用集合分别表示下列各图中的阴影部分:
|
12.已知定义在![]() 上的奇函数
上的奇函数![]() ,当
,当![]() 时,
时,![]() ,那么
,那么![]() 时,
时,![]()
13.若![]()
![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]() 的取值范围是
的取值范围是
14.函数![]()
![]() 的图象的对称轴方程为
的图象的对称轴方程为![]() ,则常数
,则常数![]()
三、解答题:
15.(12分)若集合![]()
(1)整数![]() ,
,![]() ,
,![]() 是否属于
是否属于![]() ;
;
(2)证明:一切奇数都属于![]() 。
。
16.(12分)设![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实根,又
的两个实根,又![]() ,求
,求![]() 的解析式及此函数的定义域。
的解析式及此函数的定义域。
17.(12分)设函数![]() 对任意
对任意![]() ,都有
,都有![]() ,且
,且![]() 时,
时,![]() ,
,![]() 。
。
(1)求证:![]() 是奇函数;
是奇函数;
(2)试问在![]() 时,
时,![]() 是否有最值?如果有求出最值;如果没有,说出理由.
是否有最值?如果有求出最值;如果没有,说出理由.
18.(12分)设函数![]() (
(![]() 为实数)
为实数)
(1)当![]() 时,若函数
时,若函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,求函数
对称,求函数![]() 的解析式;
的解析式;
(2)当![]() 时,求关于
时,求关于![]() 的方程
的方程![]() 在实数集
在实数集![]() 上的解。
上的解。
19.(14分)某工厂今年![]() 月、
月、![]() 月、
月、![]() 月生产某产品分别为
月生产某产品分别为![]() 万件,
万件,![]() 万件,
万件, ![]() 万件,为了估计以后每月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量
万件,为了估计以后每月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量![]() 与月份
与月份![]() 的关系,模拟函数可以选用二次函数或函数
的关系,模拟函数可以选用二次函数或函数![]() (
(![]() 、
、![]() 、
、![]() 为常数)。已知四月份该产品的产量为
为常数)。已知四月份该产品的产量为![]() 万件,请问用以上哪个函数作模拟函数较好?说明理由。
万件,请问用以上哪个函数作模拟函数较好?说明理由。
20.(14分)设函数![]() ,
,
(1)求![]() 的定义域;
的定义域;
(2)![]() 是否存在最大值或最小值?如果存在,请把它求出来;若不存在,请说明理由。
是否存在最大值或最小值?如果存在,请把它求出来;若不存在,请说明理由。
期中测试参考答案
一、DBCBD DCDDA
二、11.(1)![]() (或
(或![]() );(2)
);(2) ![]() (或
(或![]() );
);
(3) ![]() ;(4)
;(4) ![]() ;
;
12.![]() ; 13.
; 13.![]() ; 14.
; 14.![]() ;
;
三、15. 解:(1)∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
假设![]() ,
,![]() ,则
,则![]() ,且
,且![]()
∵![]() ,∴
,∴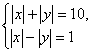 或
或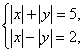 ,显然均无整数解,∴
,显然均无整数解,∴![]()
(2)设奇数为![]() ,
,![]() ,则恒有
,则恒有![]() ,∴
,∴![]() ,即一切奇数都属于
,即一切奇数都属于![]() 。
。
16. 解:∵![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实根,
的两个实根,
∴ ![]() ,解得
,解得![]() 或
或![]() 。
。
又∵![]() ,
, ![]() ,
,
∴![]()
即![]() (
(![]() 或
或![]() )。
)。
17.解:⑴证明:令![]() ,则有
,则有![]() .
.
令![]() ,则有
,则有![]() . 即
. 即![]() ,
,![]() 是奇函数.
是奇函数.
⑵任取![]() ,则
,则![]()
且![]() .
.
![]() .
. ![]() 在
在![]() 上为减函数.
上为减函数.
因此![]() 为函数的最小值,
为函数的最小值,![]() 为函数的最大值.
为函数的最大值. ![]() ,
,
![]() ,
, ![]() 函数最大值为
函数最大值为![]() ,最小值为
,最小值为![]() .
.
18.解:(1)当![]() 时,
时,![]()
设![]() 图像上任意一点
图像上任意一点![]() ,则
,则![]() 关于
关于![]() 的对称点为
的对称点为![]()
由题意![]() 在
在![]() 图像上,所以,
图像上,所以, ![]() ,即
,即![]() ;
;
(2) ![]() ,即
,即![]() ,整理,得:
,整理,得:![]()
所以![]() ,又
,又![]() ,所以
,所以 ![]()
![]()
所以![]() ,从而
,从而![]() 。
。
19.解:设二次函数为![]() ,
,
由已知得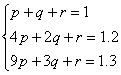 ,解之得
,解之得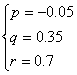
∴![]() ,当
,当![]() 时,
时,![]() .
.
又对于函数![]() ,由已知得
,由已知得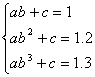 ,解之得
,解之得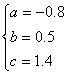
∴ ![]() 当
当 ![]() 时,
时,![]()
根据四月份的实际产量为![]() 万件,而
万件,而![]() ,
,
所以,用函数![]() 作模拟函数较好.
作模拟函数较好.
20.解:(1)由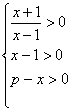 得
得![]() ,
,
因为函数的定义域是非空集合,故![]() ,所以
,所以![]() 的定义域为
的定义域为![]()
(2)∵![]()
∴当![]() ,即
,即![]() 时,
时,![]() 既无最大值又无最小值;
既无最大值又无最小值;
当![]() ,即
,即![]() 时,当
时,当![]() 时,
时,![]() 有最大值
有最大值![]() ,但没有最小值。
,但没有最小值。
综上可知:当![]() 时,
时,![]() 既无最大值又无最小值;当
既无最大值又无最小值;当![]() 时,
时,![]() 有最大值
有最大值![]() ,但没有最小值
,但没有最小值