数学必修1第一章《集合与函数概念》
高考分类练习题
一、选择题
1．已知
则
A.
B.
C. 
D．
2．设集合P={1，2，3，4}，Q={
}，则P∩Q等于
A．{1，2} B．{3，4} C．{1} D． {-2，-1，0，1，2}
3． 设函数
，区间M=[a，b](a<b)，集合N={
}，
则使M=N成立的实数对(a，b)有
A．0个 B．1个 C．2个 D．无数多个
4． 设全集是实数集R，
，
，则
等于
A. 
B. 
C. 
D．
5．函数
，其中P、M为实数集R的两个非空子集，又规定
，
，给出下列四个判断：
①若
，则
②若
，则
③若
，则
④若
，则
其中正确判断有
A. 1个 B. 2个 C. 3个 D. 4个
6设，，则
等于
A. 
B.
C. 
D.
7．设集合U={1,2,3,4,5}，A={1,3,5}，B={2,3,5}，则 
等于
A．{1，2，4} B．{4} C．{3，5}
D．
8．已知
的解析式可取为
A．
B．
C．
D．
|
|
|
对任意实数x恒成立}，则下列关系中成立的是
A．P Q B．Q P C．P=Q D．P
Q=
10．设
等于
A．{1,4} B．{1,6} C．{4,6} D．{1,4,6}
11．已知
有
A．最大值
B．最小值 C．最大值1 D．最小值1
12．函数
的定义域为
A．
B．
C．
D．
13．若f(x)=-x2+2ax与
在区间[1,2]上都是减函数，则a的值范围是
A．
B．
C．（0，1） D．
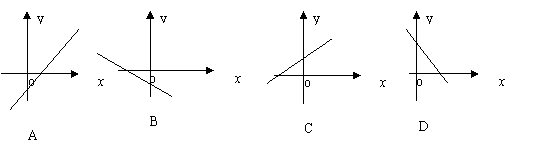
14．若函数f(x)=x2+bx+c的图象的顶点在第四象限，则函数f /(x)的图象是
15．设集合U={(x,y)x∈R,y∈R}, A={(x,y)2x-y+m>0}, B={(x,y)x+y-n≤0},
那么点P（2，3）
的充要条件是
A．
B．
C．
D．
16．设A、B、I均为非空集合，且满足A
B I，则下列各式中错误的是
A．(
A)∪B=I B．(A)∪(B)=I
C．A∩(B)= D．(A)(B)= B
17．设集合U={1，2，3，4，5}，A={1，2，3}，B={2，5}，则A∩（
B）=
A．{2} B．{2，3} C．{3} D． {1，3}
18．设集合
，
，
则集合
中元素的个数为
A.1 B.2 C.3 D.4
19．设函数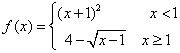
，则使得f(x)
1的自变量x的取值范围为
A．
B.
C. 
D.
20． 已知集合
，则集合
= A．{0} B．{0，1} C．{1，2} D．{0，2}
21．设函数
为奇函数，
则
A．0 B．1 C．
D．5
22．设集合U={0，1，2，3，4，5}，集合M={0，3，5}，N={1，4，5}，则M∩（
）=
A．{5} B．{0，3} C．{0，2，3，5} D. {0，1，3，4，5}
23． 设集合
，
，那么下列结论正确的是
A. 
B. 
C. 
D. 
24．若U={1,2,3,4}, M={1,2},N={2,3}, 则
=
A．{1,2,3} B．{2} C．{1,3,4} D．{4}
25．函数
, 则
A．1 B．-1
C．
D．
26．设k>1，f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中，函数y=f(x)的图
象与x轴交于A点，它的反函数y=f -1(x)的图象与y轴交于B点，并且这两个函数的图象交于P点. 已知四边形OAPB的面积是3，则k等于
A．3 B． C． D．
二、填空题
1．在函数
中，若a，b，c成等比数列且
，则
有最____________值（填“大”或“小”），且该值为__________
2．设函数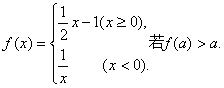
则实数a的取值范围
是 .
3．设A、B为两个集合，下列四个命题：
① A
B
对任意
② AB
③ ABA
B ④ AB存在
其中真命题的序号是 .（把符合要求的命题序号都填上）
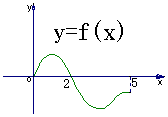4．设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,f(x)的图象如右图,则不等式f(x)<0的解是
.
5．若函数f(x)=a
在[0,+∞）上为增函数,则实数a、b的取值范围是 。
6．某日中午12时整，甲船自A处以16km/h的速度向正东行驶，乙船自A的正北18km处以24km/h的速度向正南行驶，则当日12时30分时两船之间距离对时间的变化率是 km/h.。
三、计算题
1．某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元
（I）当一次订购量为多少个时，零件的实际出厂单价恰降为51元？
（II）设一次订购量为x个，零件的实际出厂单价为P元，写出函数
的表达式；
（III）当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个，利润又是多少元？（工厂售出一个零件的利润＝实际出厂单价－成本）
[解] 本小题主要考查函数的基本知识，考查应用数学知识分析问题和解决问题的能力
（I）设每个零件的实际出厂价恰好降为51元时，一次订购量为
个，则
因此，当一次订购量为550个时，每个零件的实际出厂价恰好降为51元
（II）当
时，
当
时，
当
时，
所以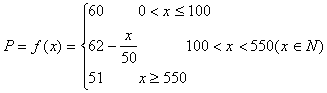
（III）设销售商的一次订购量为x个时，工厂获得的利润为L元，则
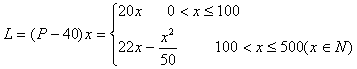
当
时，
；当
时，
因此，当销售商一次订购500个零件时，该厂获得的利润是6000元；
如果订购1000个，利润是11000元
2． 某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低0.02元根据市场调查，销售商一次订购量不会超过500件
（I）设一次订购量为x件，服装的实际出厂单价为P元，写出函数的表达式；
（II）当销售商一次订购了450件服装时，该服装厂获得的利润是多少元？
（服装厂售出一件服装的利润＝实际出厂单价－成本）
[解] 本小题主要考查函数的基本知识，考查应用数学知识分析问题和解决问题的能力
（I）当时，
当
时，
所以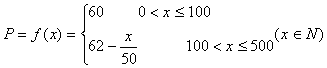
（II）设销售商的一次订购量为x件时，工厂获得的利润为L元，则
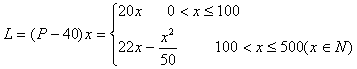
当
时，
因此，当销售商一次订购了450件服装时，该厂获利的利润是5850元
选择题与填空题答案
一、选择题
1．A 2．A 3．A 4．A 5．B 6．D 7．A 8．C
9．A 10．D 11．D 12．D 13．D 14．A 15．A 16．B
17．D 18．B 19．C 20．D 21．C 22．B 23．D 24．D
25．B 26．B
二、填空题
1． 大 -3
2． 
3． （4）
4．（－2,0）∪（2,5） 5． a>0且b≤0 6．－1.6